Задачи про динамику поступательного движения, или динамику материальной точки. Активность в теме Динамика поступательного движенияЛучшие решения в теме Динамика поступательного движенияДве материальные точки движутся согласно уравнениям
Дано:
Закон движения M
$ x = A1 + B1t + C1 t^2 $ Закон движения N
$ x^2 = A2 + C2 t^2 $ где:
таблица 3
Чтобы получить закон изменения скорости берем производную от закона движения M
$ U = (10 + 32 t - 3 t^2)' = 32 - 6t $ Чтобы получить закон изменения скорости берем производную от закона движения N
$ V = (sqrt(5 + 5 t^2))' = \frac{5t}{sqrt(5t^2+5)} $ Составляем уравнение
$ 32 - 6t = \frac{5t}{sqrt(5t^2+5)} $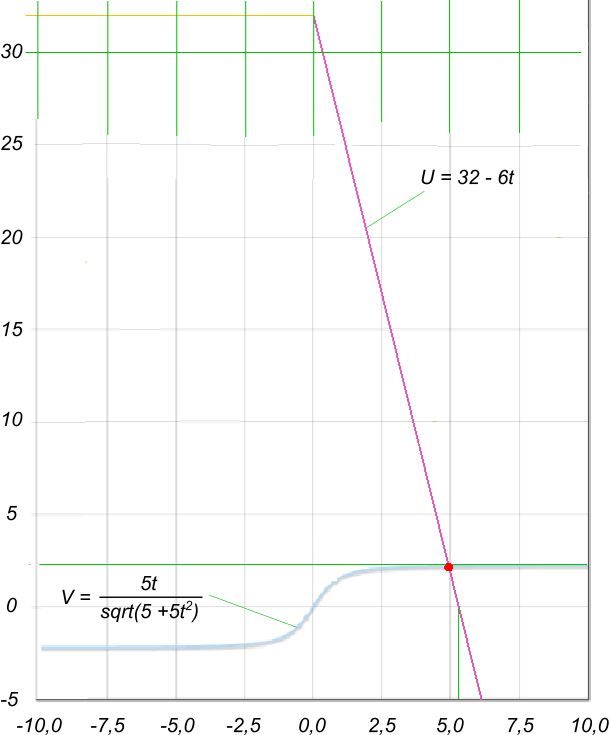 
На рисунке представлены графики скоростей. При to = 4,97 с U = V = 2,18 Чтобы получить закон изменения ускорения берем производную от закона скорости M
$ a = (32-6t)' = - 6 $ Ускорение точки M постоянно, следовательно
$ ao = - 6 \frac{м}{с^2} $ Чтобы получить закон изменения ускорения берем производную от закона скорости N
$ go = \frac{sqrt(5)}{sqrt(t^2+1)} (1 - \frac{t^2}{t^2+1}) = 0.017 \frac{м}{с^2} $ Сложнейшие задачи в теме Динамика поступательного движения Тема задачи: Динамика поступательного движения
С какой скоростью и каким курсом должен лететь самолет
9 декабря 2017 01:23
0 подписчиков
871 просмотр
0
решений Тема задачи: Динамика поступательного движения
Две материальные точки движутся согласно уравнениям
15 марта 2017 21:30
0 подписчиков
4209 просмотров
1
решение |
Записать новую задачу
Все задачи
Все темы
Все физики
Темы с решениями |
Комментарии