Какой угол наименьшего отклонения даст призма в воде?

Тема задачи: Геометрическая оптика, Линзы

Создано: @riddik 12 октября 2015 23:07

Трехгранная призма с преломляющим углом 60 градусов дает угол наименьшего отклонения в воздухе 37 градусов. Какой угол наименьшего отклонения даст призма в воде?

Оцените сложность задачи:

0 голосов, средняя сложность: 0.0000

Решения задачи

Создано: @nick 14 июля 2016 07:30

поставьте оценку:

1 голосов, средний бал: 5.0000

Дано: трехгранная призма в двух средах - водзухе и воде

Преломляющий угол призмы

град.

Показатель преломления воздуха

$n_{возд}$

Угол наименьшего отклонения призмы в воздухе

$α_{возд}^min$

град.

Показатель преломления воды

$n_{вод}$

1,33

Угол наименьшего отклонения призмы в воде

$α_{вод}^min$

Изображаем графически условие задачи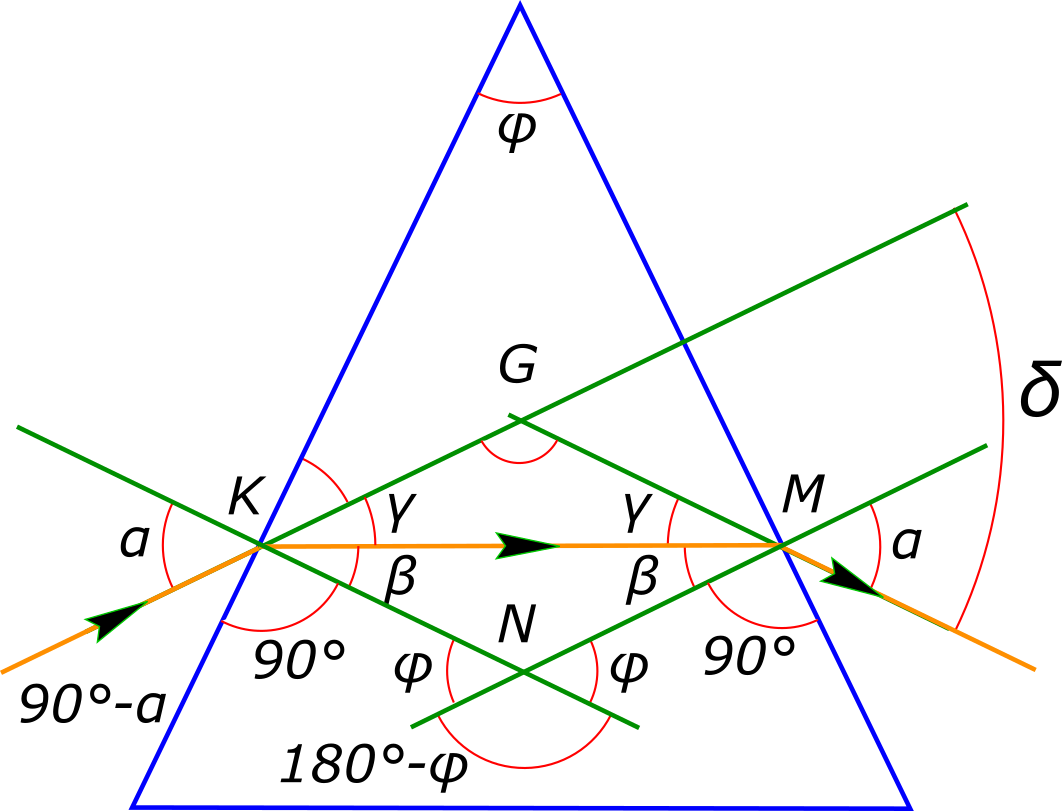

рисунок 1

Рассматривая треугольник KMN можем записать

$ N+2β=180°$ , где $N=180°-φ$, откуда $φ=2β $

Рассматривая треугольник GKM можем записать

$ G=180-2γ=180°-δ$, откуда $δ=2γ $

$ α=β+γ=\frac{φ}{2}+\frac{δ}{2} $

Угол наименьшего отклонения призмы в воздухе

$ α_{возд}=\frac{60°}{2}+\frac{37°}{2}=48,5° $

Находим значение функции

$ sinα_{возд}=sin(\frac{3,14×48,5°}{180°})=sin0,8465=0,749 $

Закон преломления света для призмы в воздухе (1)

$ \frac{sinα_{возд}}{sinβ}=\frac{n}{n_{возд}} $

Закон преломления света для призмы в воде (2)

$ \frac{sinα_{вод}}{sinβ}=\frac{n}{n_{вод}} $

Разделив первое уравнение на второе получим

$ \frac{sinα_{возд}}{sinα_{вод}}=\frac{n_{вод}}{n_{возд}} $

Откуда

$ sinα_{вод}=\frac{sinα_{возд}}{\frac{n_{вод}}{n_{возд}}}=0,749×\frac{1}{1,33}=0,563 $

Угол наименьшего отклонения призмы в воде

$ α_{вод}=arcsinα_{вод}=arcsin0,563=0,598 $

переводим радианы в градусы

$ α_{вод}=\frac{0,598×180°}{3,14}=34,3° $

Находим

$ δ=2α-φ $

тогда

$ δ_{вод}=2α_{вод}-φ=2×34,3°-60°=8,6° $

Ответ:

$ в воде угол наим. отклонения призмы составит 8,6° $

Какой угол наименьшего отклонения даст призма в воде?

Комментарии

Решения задачи

Комментарии