Найти ускорение движения бруска и силу натяжения нити

Тема задачи: Второй закон Ньютона Создано: @nick 19 июля 2017 15:47

Брусок массой 2 кг скользит по горизонтальной плоскости под действием груза массой 0,5 кг, прикрепленного к концу нерастяжимой нити, перекинутой через неподвижный блок. Коэффициент трения бруска о поверхность равен 0,1. Найти ускорение движения бруска и силу натяжения нити.

Оцените сложность задачи:
0 голосов, средняя сложность: 0.0000

Решения задачи

Создано: @nick 20 июля 2017 11:25
поставьте оценку:
1 голосов, средний бал: 5.0000

Данные задачи: брусок скользит по горизонтальной плоскости

Масса бруска$m_{1}$$2$$кг$
Масса груза$m_{2}$$0,5$$кг$
Коэффициент трения бруска о поверхность$μ$$0,1$
Ускорение движения бруска$a$$?$
Сила натяжения нити$T$$?$
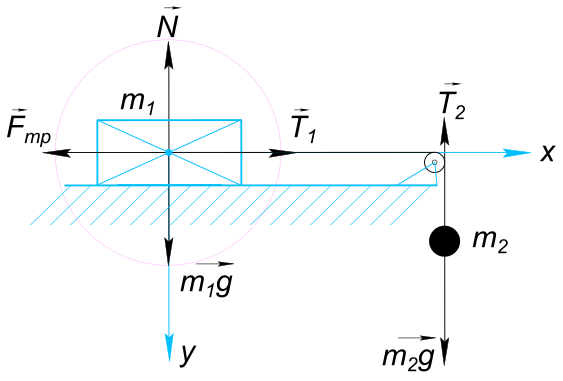
Изобразим на рисунке условия задачи

Изобразим на рисунке условия задачи

На брусок действуют силы:

Сила тяжести

$ m_{1}g $

Сила нормальной реакции опоры

$ N $

Сила натяжения нити

$ T_{1} $

Сила трения

$ F_{тр} $

На груз действуют силы:

Сила тяжести

$ m_{2}g $

Сила натяжения нити

$ T_{1} $

Запишем для бруска и для груза уравнения в векторной форме

$ \vect{m_{1}g}+\vect{N_{}}+\vect{T_{1}}+\vect{F_{тр}} = \vect{m_{1}a_{1}} $

$ \vect{m_{2}g}+\vect{T_{2}} = \vect{m_{2}a_{2}} $

Спроецируем силы действующие на брусок на выбранные направления осей x и y, получим:

ось x:

$ T_{1}-F_{тр} = m_{1}a_{1} $

ось y:

$ m_{1}g - N = 0 $

Из уравнения для оси y

$ m_{1}g = N $

Поэтому

$ F_{тр} = μN = μm_{1}g $

Тогда уравнение для оси x принимает вид

$ T_{1}-μm_{1}g = m_{1}a_{1} $

Спроецируем силы действующие на груз на направление оси y, получим:

ось y:

$ m_{2}g - T_{2} = m_{2}a_{2} $

Так как нить невесомая и нерастяжимая, а масса блока пренебрежимо мала, поэтому

$ T_{1} = T_{2} = T $

и

$ |a_{1}| = |a_{2}| = a $

Тогда уравнения для бруска и для груза принимаю вид

$ T - μm_{1}g = m_{1}a $

$ m_{2}g - T = m_{2}a $

Решаем их как систему уравнений:

$ m_{2}g - m_{2}a = T $

тогда

$ m_{2}g - m_{2}a - μm_{1}g = m_{1}a $

и

$ (m_{2} - μm_{1})g = (m_{2}+m_{1})a $

откуда

$ a = \frac{(m_{2} - μm_{1})g}{m_{2}+m_{1}}=\frac{(0,5 - 0,1×2)×10}{0,5+2}=1,2 \frac{м}{с^{2}} $

и

$ T = m_{2}(g - a) = 0,5×(10 - 1,2) = 4,4 Н $

Ответ:

$ Ускорение движения бруска 1,2 \frac{м}{с^{2}} $

и

$ Сила натяжения нити 4,4 Н $

Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь

 Записать новую задачу Все задачи Все темы Все физики