Задачи про второй закон Ньютона Активность в теме Второй закон НьютонаСамые активные физики в теме Второй закон НьютонаЛучшие решения в теме Второй закон НьютонаНайти ускорение движения бруска и силу натяжения нити
Данные задачи: брусок скользит по горизонтальной плоскости
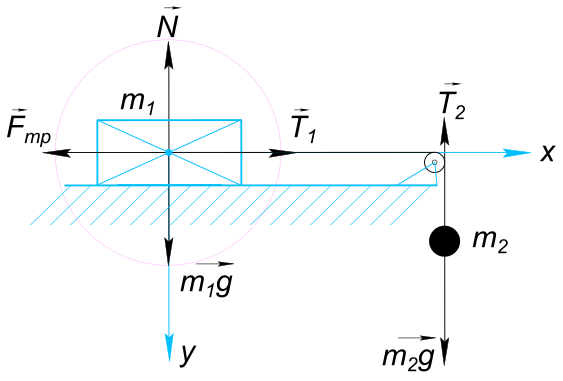
Изобразим на рисунке условия задачи На брусок действуют силы: Сила тяжести
$ m_{1}g $ Сила нормальной реакции опоры
$ N $ Сила натяжения нити
$ T_{1} $ Сила трения
$ F_{тр} $ На груз действуют силы: Сила тяжести
$ m_{2}g $ Сила натяжения нити
$ T_{1} $ Запишем для бруска и для груза уравнения в векторной форме
$ \vect{m_{1}g}+\vect{N_{}}+\vect{T_{1}}+\vect{F_{тр}} = \vect{m_{1}a_{1}} $
$ \vect{m_{2}g}+\vect{T_{2}} = \vect{m_{2}a_{2}} $ Спроецируем силы действующие на брусок на выбранные направления осей x и y, получим: ось x:
$ T_{1}-F_{тр} = m_{1}a_{1} $ ось y:
$ m_{1}g - N = 0 $ Из уравнения для оси y
$ m_{1}g = N $ Поэтому
$ F_{тр} = μN = μm_{1}g $ Тогда уравнение для оси x принимает вид
$ T_{1}-μm_{1}g = m_{1}a_{1} $ Спроецируем силы действующие на груз на направление оси y, получим: ось y:
$ m_{2}g - T_{2} = m_{2}a_{2} $ Так как нить невесомая и нерастяжимая, а масса блока пренебрежимо мала, поэтому
$ T_{1} = T_{2} = T $ и
$ |a_{1}| = |a_{2}| = a $ Тогда уравнения для бруска и для груза принимаю вид
$ T - μm_{1}g = m_{1}a $
$ m_{2}g - T = m_{2}a $ Решаем их как систему уравнений:
$ m_{2}g - m_{2}a = T $ тогда
$ m_{2}g - m_{2}a - μm_{1}g = m_{1}a $ и
$ (m_{2} - μm_{1})g = (m_{2}+m_{1})a $ откуда
$ a = \frac{(m_{2} - μm_{1})g}{m_{2}+m_{1}}=\frac{(0,5 - 0,1×2)×10}{0,5+2}=1,2 \frac{м}{с^{2}} $ и
$ T = m_{2}(g - a) = 0,5×(10 - 1,2) = 4,4 Н $ Ответ:
$ Ускорение движения бруска 1,2 \frac{м}{с^{2}} $ и
$ Сила натяжения нити 4,4 Н $ Какую наименьшую скорость, в верхней точке «мертвой петли» должен иметь самолет, чтобы не свалиться в «штопор»
Данные задачи: самолет выполняет «мертвую петлю»
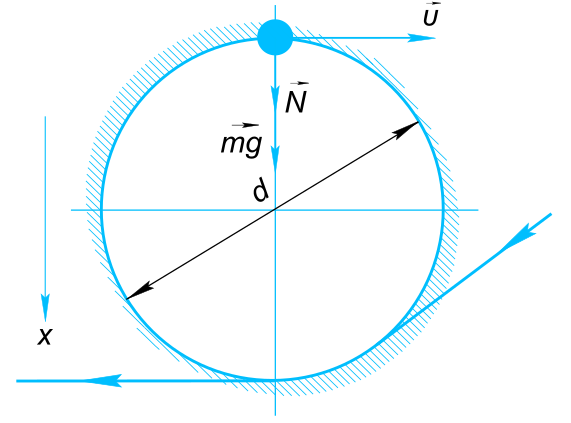
Изобразим на рисунке условия задачи В верхней точке на самолет действует сила тяжести
$ \vect{mg} $ и реакция опоры (самолет летит опираясь крыльями на воздух)
$ \vect{N} $ Направим ось x вертикально вниз и запишем уравнение движения самолета в проекции на данную ось
$ N+mg = ma $ Где
$ a - центробежное ускорение $ В момент прохождения верхней точки самолет и летчик находятся в состоянии невесомости
$ N = 0 $ И тогда
$ mg = ma $ Где
$ a = \frac{υ^{2}}{R}=\frac{υ^{2}}{\frac{d}{2}} $ Откуда находим
$ υ = \sqrt{g\frac{d}{2}}=\sqrt{9,81\frac{510}{2}}=50 \frac{м}{с} $ Ответ:
$ наименьшая скорость самолета равна 50 \frac{м}{с} $ КомментарииНайдите работу силы трения.
Дано:
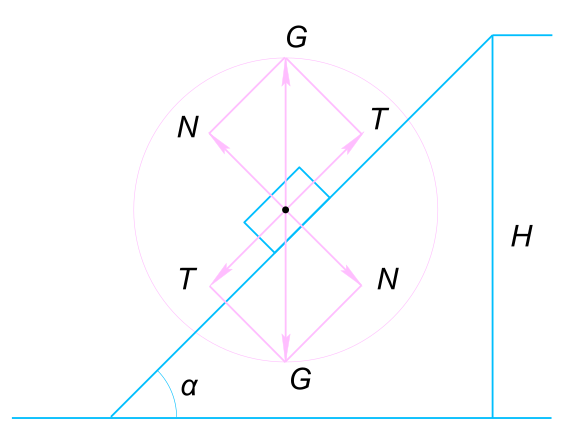
Изображаем на рисунке условия задачи Составляем уравнение для работы силы трения
$ W = N f S = f S G cos α $ Составляем уравнение
$ sin α = \frac{H}{S} $ Откуда находим путь проделанный телом по наклонной плоскости
$ S = \frac{H}{sin α} $ Тогда работа силы трения
$ W = f \frac{H}{sin α} G cos α = \frac{fGH}{tg α} = \frac{0,2 × 0,5 × 9,81 × 7}{1} = 6,87 Дж $ КомментарииОпределить кинетическую энергию цилиндра и время остановки.
Пример текста Данные задачи: Сплошной цилиндр массой катится без скольжения с постоянной скоростью
Анализируем условие задачи: Цилиндр имеет два состояния - катится и остановился; Остановка цилиндра наступает в результате приложения к нему силы F=50 Н; Кинетическая энергия цилиндра растрачивается на преодоление работы силы F. Составляем уравнение
$ \frac{1}{2}mv^2 - FS = 0 $ Где S - путь, пройденный цилиндром до его остановки Кинетическая энергия цилиндра до момента приложения силы F
$ \frac{1}{2}mv^2 = \frac{1}{2}×10×10^2 = 500 дж $ Составляем уравнение
$ F = ma $ Где a - ускорение вызываемое силой F Откуда
$ a = \frac{F}{m} $ Составляем уравнение пути пройденного цилиндром
$ S = \frac{1}{2F}mv^2 $ Составляем уравнение пути пройденного цилиндром
$ S = at^2 $ Тогда
$ t^2 = \frac{1}{2Fa}mv^2 $ или
$ t = sqrt{\frac{1}{2F}mv^2\frac{m}{F}} = \frac{mv}{F}sqrt{\frac{1}{2}} = 1,77 с $ Ответ:
$ Кинетическая энергия цилиндра 500 дж, t = 1,77 с $ КомментарииС какой силой нужно действовать на тело, чтобы оно падало вертикально вниз с ускорением 15 м/c2
Данные задачи: тело падает вертикально вниз
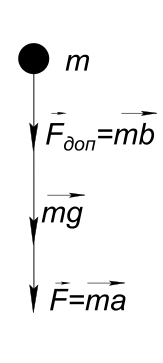
Изобразим на рисунке условия задачи На тело действуют две силы
$ Σ\vect{F} = \vect{mg}+\vect{mb} $ где
$ b - ускорение от силы F_{доп} $ Тогда
$ ma = mg+mb $ Откуда
$ b = a-g $ Тогда
$ F_{доп} = m(a-g)= 5(15-10)=25 Н $ Ответ:
$ на тело нужно действовать вниз силой 25 Н $ КомментарииСложнейшие задачи в теме Второй закон Ньютона Тема задачи: Второй закон Ньютона
Какую наименьшую скорость, в верхней точке «мертвой петли» должен иметь самолет, чтобы не свалиться в «штопор» Тема задачи: Второй закон Ньютона
Какую наименьшую скорость, в верхней точке «мертвой петли» должен иметь самолет, чтобы не свалиться в «штопор»
25 июля 2017 13:57
0 подписчиков
2696 просмотров
1
решение  Тема задачи: Второй закон Ньютона
Найдите работу силы трения. Тема задачи: Второй закон Ньютона
Найдите работу силы трения.
1 декабря 2016 21:34
0 подписчиков
3440 просмотров
1
решение  Тема задачи: Второй закон Ньютона
Определить кинетическую энергию цилиндра и время остановки. Тема задачи: Второй закон Ньютона
Определить кинетическую энергию цилиндра и время остановки.
1 декабря 2016 21:36
0 подписчиков
5514 просмотра
1
решение  Тема задачи: Второй закон Ньютона
С какой силой нужно действовать на тело, чтобы оно падало вертикально вниз с ускорением 15 м/c2 Тема задачи: Второй закон Ньютона
С какой силой нужно действовать на тело, чтобы оно падало вертикально вниз с ускорением 15 м/c2
19 июля 2017 11:39
0 подписчиков
2511 просмотр
1
решение  Тема задачи: Второй закон Ньютона
Определить величину и направление ускорения лифта Тема задачи: Второй закон Ньютона
Определить величину и направление ускорения лифта
19 июля 2017 14:02
0 подписчиков
5650 просмотров
1
решение |
Записать новую задачу
Все задачи
Все темы
Все физики
Темы с решениями |





Комментарии