Цепи постоянного тока Задачи

6 Задач в теме

7 Решений в теме

0 Подписчиков

О теме Новые Задачи Интересные Задачи Без Решения Интересующиеся

Задачи про цепи постоянного тока

Активность в теме Цепи постоянного тока

Самые активные физики в теме Цепи постоянного тока

Лучшие решения в теме Цепи постоянного тока

Найти силу тока в резисторе с меньшим сопротивлением

Создано: @nick 20 июня 2016 19:31

поставьте оценку:

2 голосов, средний бал: 5.0000

R1=6 Ом R2=9 Ом P2= 36 Вт I1= ? $P=RI^2$

$I_2=(\frac{P_2}{R_2})^{0,5}=(\frac{36}{9})^{0,5}=\frac{6}{3}=2[А]$

$U_2=U_1$

$I_1×R_1=I_2×R_2$

$I_1 =I_2\frac{R_2}{R_1}=2\frac{9}{6}=3[А]$

Ответ: сила тока в резисторе с меньшим сопротивлением равна 3 А.

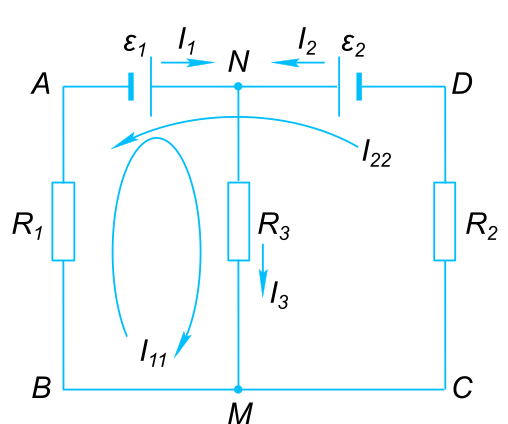
На рисунке изображена замкнутая электрическая цепь. Для нее принято считать, что ток течет от плюса к минусу. В электрическую цепь включены два источника питания. Если источники включены навстречу друг другу (т.е. их полярности противоположны), то их ЭДС вычитаются.

1-й этап. Согласно первому закону Кирхгофа алгебраическая сумма токов в ветвях цепи, соединенных электрическим узлом равна нулю. Для узла N имеем

$ ( I_{1})+(I_{2})+(-I_{3})=0 $

или

$ I_{3}=I_{1}+ I_{2} $

Для решения задачи используем метод контурных токов, в котором на основании второго закона Кирхгоффа выполняем определение значений контурных токов, замыкающихся в независимых контурах. Выберем и рассмотрим два контура ABCD и ABMN, для каждого из них выберем направление обхода. Предположительно определим направление токов в каждом сопротивлении. Для контура ABMN имеем.

$ ε_{1}=I_{3}R_{3}+I_{1}R_{1} $

Для контура ABCD Для контура 2

$ ε_{2}-ε_{1}=I_{2}R_{2}-I_{3}R_{3} $

2-й этап. Из уравнения (1)

$ I_{3}=\frac{ε_{1}-I_{1}R_{1}}{R_{3}} $

А из уравнения (2)

$ I_{2}=\frac{ε_{2}-ε_{1}+I_{1}R_{1}}{R_{2}} $

Тогда

$ I_{1}=I_{3}-I_{2}=\frac{ε_{1}-I_{1}R_{1}}{R_{3}}-\frac{ε_{2}-ε_{1}+I_{1}R_{1}}{R_{2}} $

Решаем уравнение относительно I_{1}

$I_{1}R_{3}R_{1}=ε_{1}R_{2}-I_{1}R_{1}R_{2}-ε_{2}R_{3}+ε_{1}R_{3}-I_{1}R_{1}R_{3}$

$I_{1}(R_{3}R_{2}+R_{1}R_{2}+R_{1}R_{3})=ε_{1}R_{2}-ε_{2}R_{3}+ε_{1}R_{3}$