Задачи про первый закон Ньютона Активность в теме Первый закон НьютонаСамые активные физики в теме Первый закон НьютонаЛучшие решения в теме Первый закон НьютонаОпределить скорость движения пули
Данные задачи: пуля пробивает вагон насквозь
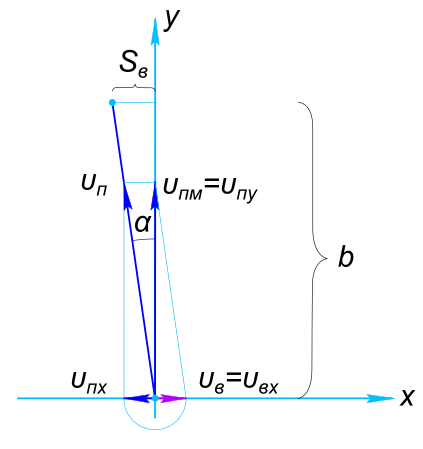
Изобразим на рисунке условия задачи Согласно закону прямолинейного равномерного поступательного движения составляем уравнение
$ \frac{S_{в}}{υ_{в}} =\frac{S_{п}}{υ_{п}}= t $ Путь пули
$ S_{п}=\sqrt{b^{2}+(S_{в})^{2}}=\sqrt{(3,6)^{2}+(0,18)^{2}}=3,6045 м $ Из уравнения находим
$ υ_{п} = \frac{S_{п}υ_{в}}{S_{в}}=\frac{3,6045×15}{0,18}=300,375 \frac{м}{с} $ Ответ:
$ Скорость движения пули 300,375 \frac{м}{с} $ Определить скорость лодки и скорость течения реки
Данные задачи: лодка переплывает реку
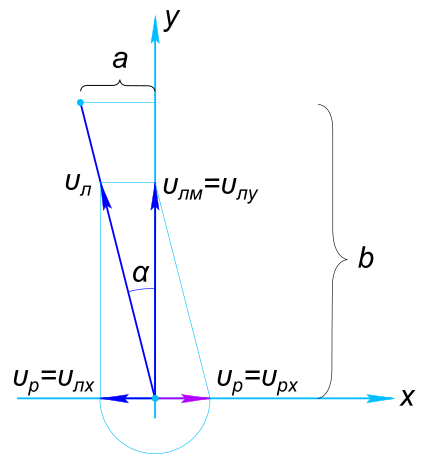
Изобразим на рисунке условие задачи За время пути перемещение лодки складывается из двух взаимно перпендикулярных перемещений - поперек реки и вдоль реки
$ \vect{S_{л}} = \vect{S_{x}}+\vect{S_{y}} $ Согласно закону прямолинейного равномерного поступательного движения составляем уравнение
$ \frac{b}}{υ_{лм}}= \frac{S_{x}}{υ_{р}}=t $ Откуда находим
$ υ_{р} = \frac{S_{a}}{t}=\frac{25}{100}=0,25 \frac{м}{с} $ и
$ υ_{лм} = \frac{b}{t}=\frac{100}{100}=1 \frac{м}{с} $ Тогда
$ υ_{л} = \sqrt{(υ_{лм})^{2}+(υ_{р})^{2}}=\sqrt{(1)^{2}+(0,25})^{2}}=1,03 \frac{м}{с} $ Ответ:
$ Скорость реки 1 \frac{м}{с}, а скорость лодки 1,03 \frac{м}{с} $ КомментарииОпределить положения центра тяжести стержня
Данные задачи: Стержень одинакового поперечного сечения, состоящий из двух равных частей - железной и свинцовой
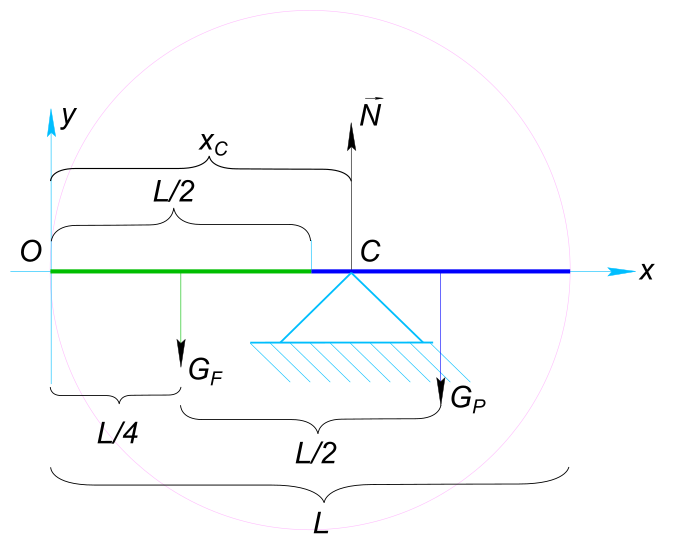
Изобразим на рисунке условия задачи Лестница находится в равновесии, тогда для сил лежащих в одной плоскости (изображенных на рисунке) должны выполняться следующие условия:
$ Σ\vect{F_{x}} = 0 $
$ Σ\vect{F_{y}} = 0 $
$ M\vect{F_{y}} = 0 $ Откуда:
$ G_{F}+G_{P} = N $ Где вес железной половины стержня
$ G_{F} = ρ_{F}\frac{L}{2}Sg $ Где вес свинцовой половины стержня
$ G_{P} = ρ_{P}\frac{L}{2}Sg $ Моменты относительно начала координат
$ M_{G_{F}}+M_{G_{P}} = M_{N} $ или
$ ρ_{F}\frac{L}{2}Sg\frac{L}{4}+ρ_{F}\frac{L}{2}Sg\frac{3L}{4} = (ρ_{F}\frac{L}{2}Sg+ρ_{P}\frac{L}{2}Sg)x_{C} $ Откуда
$ x_{C} = \frac{(ρ_{F}\frac{1}{4}+ρ_{P}\frac{3}{4})L}{ρ_{F}+ρ_{P}}=\frac{(7,9\frac{1}{4}+11,3\frac{3}{4})0,4}{7,9+11,3}=0,218 м $ Ответ:
От свинцового конца до центра тяжести 0,182 м $ КомментарииНайти жёсткость пружины
Пример текста Данные задачи: Брусок с помощью горизонтальной пружины тянут равномерно по доске, расположенной горизонтально
Анализируем условие задачи: - брусок движется равномерно; - на брусок действует сила трения и сила натяжения пружины. Для решения задачи применяем Первый закон Ньютона - тело движется прямолинейно и равномерно, или находится в состоянии покоя, если результирующая всех действующих на тело сил равна нулю. Составляем уравнение
$ Fпр - Fтр = sD - fmg =0 $ Откуда находим жесткость пружины
$ D = \frac{fmg}{s} = \frac{0,25×3×9,81}{0,05} = 147,15 \frac{Н}{м} $ Ответ: жесткость пружины равна
$ D = 147,15 \frac{Н}{м} $ КомментарииС какой скоростью и по какому курсу должен лететь самолет
Данные задачи: прокладка курса самолета
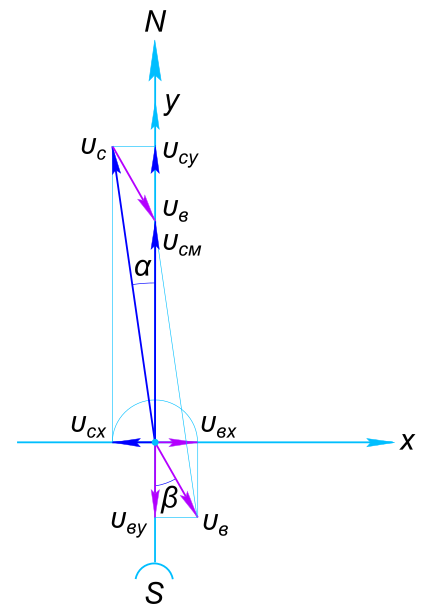
Изобразим на рисунке условия задачи Уравнение пройденного пути при равномерном поступательном движении
$ S = (ν_{сy}-ν_{вy})t $ Откуда находим скрость
$ ν_{сy} = ν_{см}+ν_{вy}=\frac{S}{t}+ν_{в}cos(β)=\frac{500}{2}+30×0,866=276 \frac{км}{ч}$ Проекция скорости на ось x
$ ν_{сx} = ν_{вx}=ν_{в}sin(β)=30×sin(\frac{π}{6})=15 \frac{км}{ч}$ Скорость самолета
$ν_{с}=\sqrt{(ν_{сy})^{2}+(ν_{сx})^{2}}=\sqrt{76176+225}=276,41 \frac{км}{ч} $ Находим курс самолета
$ sin(α) = \frac{ν_{сx}}{ν_{с}}=\frac{15}}{276,41}=0.054 $ определяем угол α
$ arcsin(α) = arcsin(0.054)=0.054 рад $ Переводим в градусы
$ α = \frac{0.054×180}{π}=\frac{0.054×180}{3,14}=3,1 град $ Ответ:
$ Скорость самолета 276 \frac{км}{ч}, а курс 3,1° на С_З $ КомментарииСложнейшие задачи в теме Первый закон Ньютона Тема задачи: Первый закон Ньютона
Определить веса грузов G2 и G3
20 сентября 2022 16:02
0 подписчиков
235 просмотров
0
решений Тема задачи: Первый закон Ньютона
Найти жёсткость пружины
1 декабря 2016 21:32
0 подписчиков
2632 просмотра
1
решение Тема задачи: Первый закон Ньютона
С какой скоростью и по какому курсу должен лететь самолет
15 июля 2017 14:41
0 подписчиков
5086 просмотров
1
решение Тема задачи: Первый закон Ньютона
Определить скорость движения пули
16 июля 2017 08:45
0 подписчиков
1670 просмотров
1
решение Тема задачи: Первый закон Ньютона
Определить скорость лодки и скорость течения реки
17 июля 2017 08:45
0 подписчиков
2735 просмотров
1
решение |
Записать новую задачу
Все задачи
Все темы
Все физики
Темы с решениями |
Комментарии