Задачи по оптике с линзами Активность в теме Геометрическая оптика, ЛинзыСамые активные физики в теме Геометрическая оптика, ЛинзыЛучшие решения в теме Геометрическая оптика, ЛинзыНайти величину бокового смещения луча
Дано: H=6 см; α=60°=π/3; $n_{возд}$=1; $n_{ст}$=1,57 h=?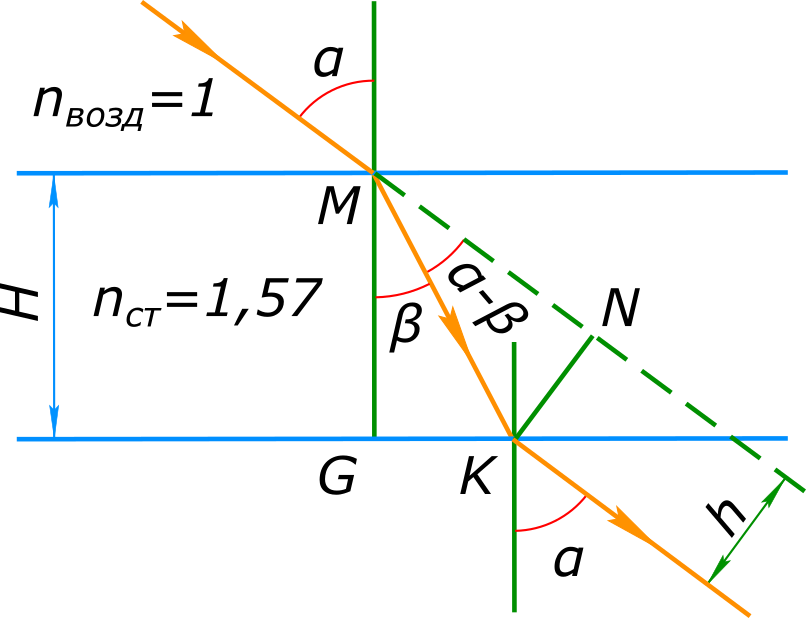 
Изобразим графически условие задачи Решение: Согласно закону преломления света $\frac{sinα}{sinβ}=\frac{n_{ст}}{n_{возд}}$, откуда $sinβ=\frac{n_{возд}sinα}{n_{ст}}=\frac{1×0,866}{1,57}$=0,5516, откуда $β=arcsin0,5516$=0,5843 Из треугольника MGK находим $cosβ=\frac{MG}{MK}$, откуда $MK=\frac{MG}{cosβ}$ Из треугольника MKN находим $sin(α-β)=\frac{KN}{MK}$, откуда $h=KN=MKsin(α-β)=\frac{MGsin(α-β)}{cosβ}=\frac{6sin(\frac{π}{3}-0,5843)}{cos0,5843}=\frac{6×0,4465}{0,834}$=3,2 см. Ответ: величина бокового смещения луча составит 3,2 см. При каком значении угла падения луч, отраженный от поверхности воды будет перпендикулярен к преломленному лучу?
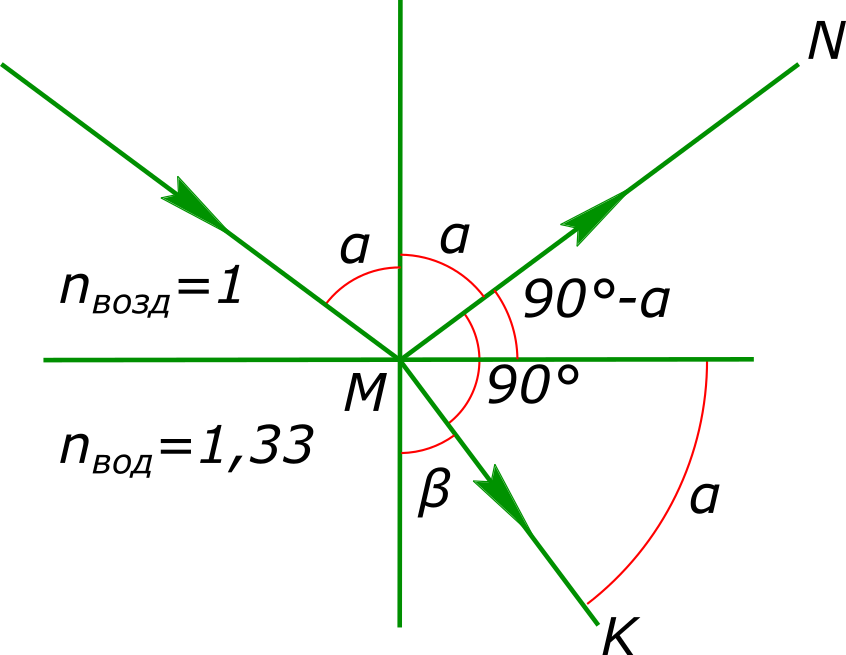
Изобразим условия задачи на рисунке Данные задачи: луч света падает на поверхность воды
Согласно закону преломления света
$\frac{sinα}{sinβ}=\frac{n_{вод}}{n_{возд}}$ из рисунка находим
$ β=90°- α $ тогда
$sinβ=sin(90°-α)=cosα$ подставляем в уравнение
$\frac{sinα}{cosα}=\frac{n_{вод}}{n_{возд}}$ вычисляем
$ tgα=1,33 $ получим значение угла падения
$ α=arctgα=arctg1,33=0,926 рад $ радианную меру переведем в градусную
$ α=\frac{0,926×180°}{3,14}=53° $ Ответ: При значении угла падения 53°.
$ При значении угла падения 53° $ КомментарииКакой угол наименьшего отклонения даст призма в воде?
Дано: трехгранная призма в двух средах - водзухе и воде
Изображаем графически условие задачи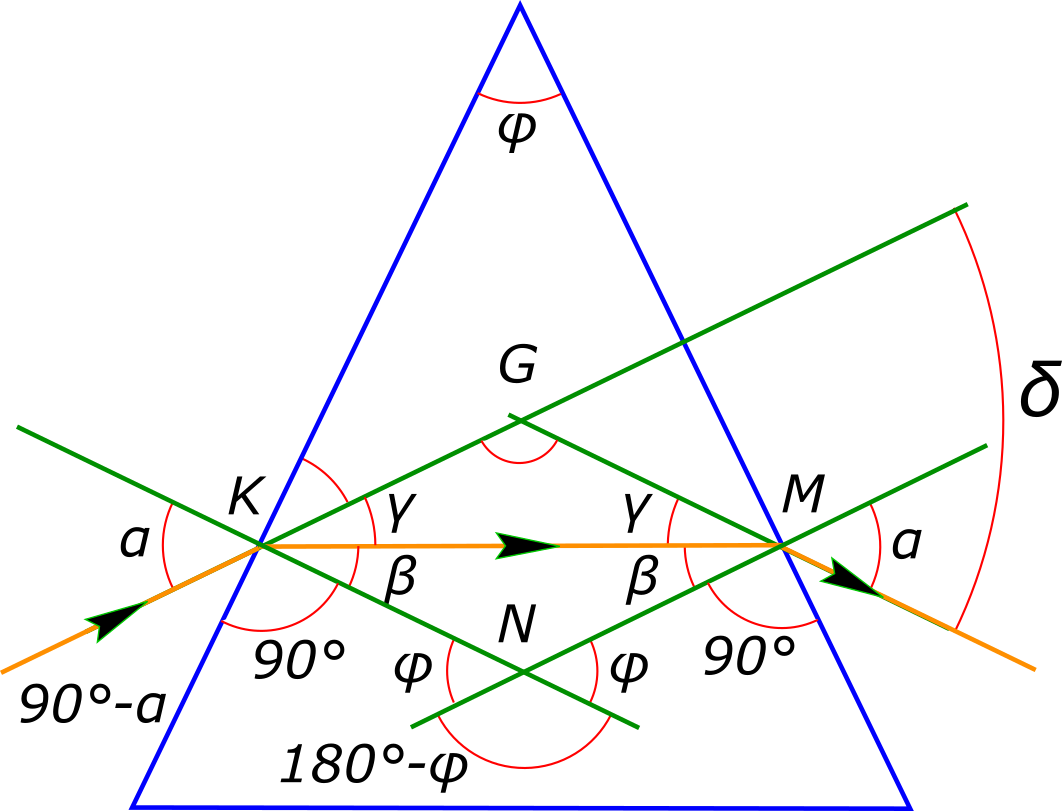 
рисунок 1 Рассматривая треугольник KMN можем записать
$ N+2β=180°$ , где $N=180°-φ$, откуда $φ=2β $ Рассматривая треугольник GKM можем записать
$ G=180-2γ=180°-δ$, откуда $δ=2γ $ и
$ α=β+γ=\frac{φ}{2}+\frac{δ}{2} $ Угол наименьшего отклонения призмы в воздухе
$ α_{возд}=\frac{60°}{2}+\frac{37°}{2}=48,5° $ Находим значение функции
$ sinα_{возд}=sin(\frac{3,14×48,5°}{180°})=sin0,8465=0,749 $ Закон преломления света для призмы в воздухе (1)
$ \frac{sinα_{возд}}{sinβ}=\frac{n}{n_{возд}} $ Закон преломления света для призмы в воде (2)
$ \frac{sinα_{вод}}{sinβ}=\frac{n}{n_{вод}} $ Разделив первое уравнение на второе получим
$ \frac{sinα_{возд}}{sinα_{вод}}=\frac{n_{вод}}{n_{возд}} $ Откуда
$ sinα_{вод}=\frac{sinα_{возд}}{\frac{n_{вод}}{n_{возд}}}=0,749×\frac{1}{1,33}=0,563 $ Угол наименьшего отклонения призмы в воде
$ α_{вод}=arcsinα_{вод}=arcsin0,563=0,598 $ переводим радианы в градусы
$ α_{вод}=\frac{0,598×180°}{3,14}=34,3° $ Находим
$ δ=2α-φ $ тогда
$ δ_{вод}=2α_{вод}-φ=2×34,3°-60°=8,6° $ Ответ:
$ в воде угол наим. отклонения призмы составит 8,6° $ КомментарииНа каком наименьшем расстоянии следует встать фотографу?
Данные задачи: Фотографирование высокого здания
Фокусное расстояние объектива определяется формуле
$ f=L\frac{h}{H} $ Откуда находим
$L=f\frac{H}{h}=50\frac{210000}{24}=43750 мм$ Ответ:
Расстояние до здания должно быть не менее 43,75 м КомментарииСложнейшие задачи в теме Геометрическая оптика, Линзы Тема задачи: Геометрическая оптика, Линзы
При каком значении угла падения луч, отраженный от поверхности воды будет перпендикулярен к преломленному лучу?
12 октября 2015 23:05
0 подписчиков
8111 просмотр
1
решение Тема задачи: Геометрическая оптика, Линзы
Найти величину бокового смещения луча
12 октября 2015 22:59
0 подписчиков
4079 просмотров
1
решение Тема задачи: Геометрическая оптика, Линзы
Какой угол наименьшего отклонения даст призма в воде?
12 октября 2015 23:07
0 подписчиков
7934 просмотра
1
решение Тема задачи: Геометрическая оптика, Линзы
Покажите, что луч света, последовательно отразившийся от трех взаимноперпендикулярных плоских зеркал, изменит свое направление на прямо противоположное
12 октября 2015 22:59
0 подписчиков
2616 просмотров
0
решений Тема задачи: Геометрическая оптика, Линзы
На каком наименьшем расстоянии следует встать фотографу?
27 октября 2015 01:41
0 подписчиков
6135 просмотров
1
решение |
Записать новую задачу
Все задачи
Все темы
Все физики
Темы с решениями |
Комментарии