Все решения физика @NICKОпределить положения центра тяжести стержня
Данные задачи: Стержень одинакового поперечного сечения, состоящий из двух равных частей - железной и свинцовой
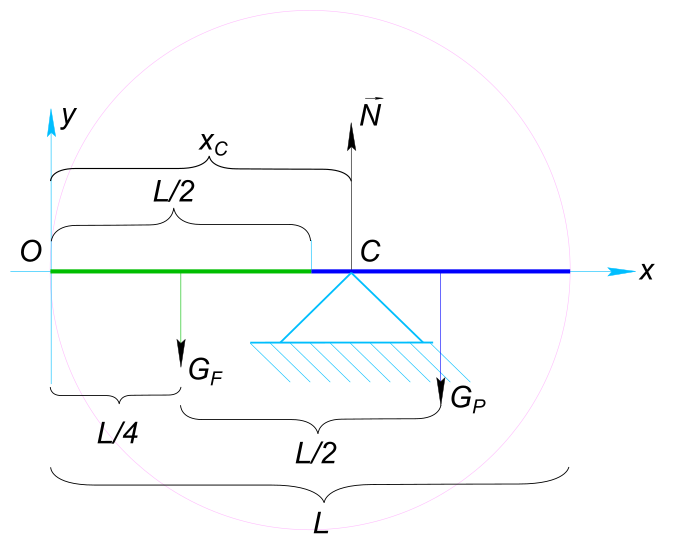
Изобразим на рисунке условия задачи Лестница находится в равновесии, тогда для сил лежащих в одной плоскости (изображенных на рисунке) должны выполняться следующие условия:
$ Σ\vect{F_{x}} = 0 $
$ Σ\vect{F_{y}} = 0 $
$ M\vect{F_{y}} = 0 $ Откуда:
$ G_{F}+G_{P} = N $ Где вес железной половины стержня
$ G_{F} = ρ_{F}\frac{L}{2}Sg $ Где вес свинцовой половины стержня
$ G_{P} = ρ_{P}\frac{L}{2}Sg $ Моменты относительно начала координат
$ M_{G_{F}}+M_{G_{P}} = M_{N} $ или
$ ρ_{F}\frac{L}{2}Sg\frac{L}{4}+ρ_{F}\frac{L}{2}Sg\frac{3L}{4} = (ρ_{F}\frac{L}{2}Sg+ρ_{P}\frac{L}{2}Sg)x_{C} $ Откуда
$ x_{C} = \frac{(ρ_{F}\frac{1}{4}+ρ_{P}\frac{3}{4})L}{ρ_{F}+ρ_{P}}=\frac{(7,9\frac{1}{4}+11,3\frac{3}{4})0,4}{7,9+11,3}=0,218 м $ Ответ:
От свинцового конца до центра тяжести 0,182 м $ Под каким наименьшим углом к горизонту можно прислонить лестницу к гладкой вертикальной стене
Данные задачи: Лестница прислонена к гладкой вертикальной стене
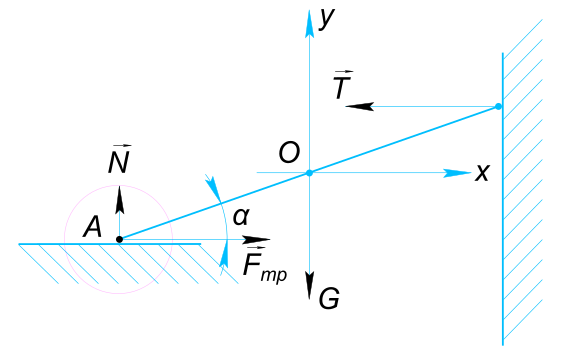
Изобразим на рисунке условия задачи Лестница находится в равновесии, тогда для сил лежащих в одной плоскости и изображенных на рисунке должны выполняться следующие условия:
$ Σ\vect{F_{x}} = 0 $
$ Σ\vect{F_{y}} = 0 $
$ Σ\vect{M_{A}} = 0 $ Откуда:
$ F_{тр} = T $
$ N = G $
$ TLsin(α) = G\frac{L}{2}cos(α) $ Откуда
$ tg(α) = \frac{G}{2T}=\frac{G}{2G0,4}=\frac{1}{2×0,4}=1,25 $ тогда
$ arctg(α) = arctg(1,25)=0,896 рад.$ Переводим радианы в градусную меру
$ α = \frac{0,896×180}{3,14}= 51,36 град. $ Ответ:
$ Минимальный угол лестницы к горизонту 51,36 ° $ КомментарииОпределить скорость лодки и скорость течения реки
Данные задачи: лодка переплывает реку
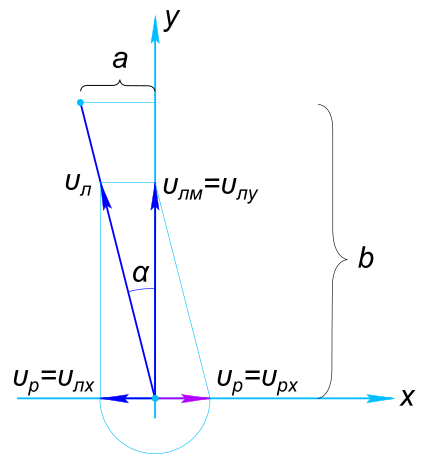
Изобразим на рисунке условие задачи За время пути перемещение лодки складывается из двух взаимно перпендикулярных перемещений - поперек реки и вдоль реки
$ \vect{S_{л}} = \vect{S_{x}}+\vect{S_{y}} $ Согласно закону прямолинейного равномерного поступательного движения составляем уравнение
$ \frac{b}}{υ_{лм}}= \frac{S_{x}}{υ_{р}}=t $ Откуда находим
$ υ_{р} = \frac{S_{a}}{t}=\frac{25}{100}=0,25 \frac{м}{с} $ и
$ υ_{лм} = \frac{b}{t}=\frac{100}{100}=1 \frac{м}{с} $ Тогда
$ υ_{л} = \sqrt{(υ_{лм})^{2}+(υ_{р})^{2}}=\sqrt{(1)^{2}+(0,25})^{2}}=1,03 \frac{м}{с} $ Ответ:
$ Скорость реки 1 \frac{м}{с}, а скорость лодки 1,03 \frac{м}{с} $ КомментарииОпределить скорость движения пули
Данные задачи: пуля пробивает вагон насквозь
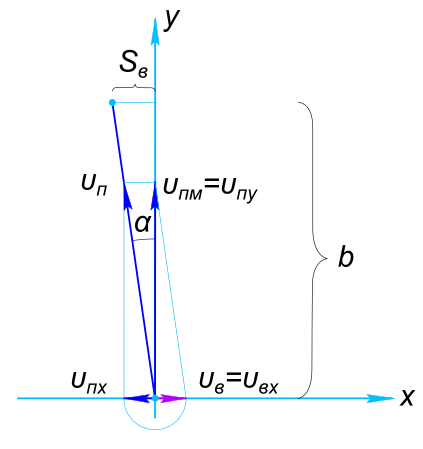
Изобразим на рисунке условия задачи Согласно закону прямолинейного равномерного поступательного движения составляем уравнение
$ \frac{S_{в}}{υ_{в}} =\frac{S_{п}}{υ_{п}}= t $ Путь пули
$ S_{п}=\sqrt{b^{2}+(S_{в})^{2}}=\sqrt{(3,6)^{2}+(0,18)^{2}}=3,6045 м $ Из уравнения находим
$ υ_{п} = \frac{S_{п}υ_{в}}{S_{в}}=\frac{3,6045×15}{0,18}=300,375 \frac{м}{с} $ Ответ:
$ Скорость движения пули 300,375 \frac{м}{с} $ КомментарииС какой скоростью и по какому курсу должен лететь самолет
Данные задачи: прокладка курса самолета
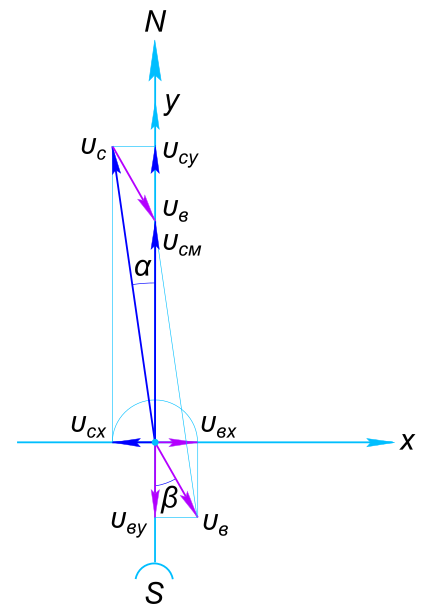
Изобразим на рисунке условия задачи Уравнение пройденного пути при равномерном поступательном движении
$ S = (ν_{сy}-ν_{вy})t $ Откуда находим скрость
$ ν_{сy} = ν_{см}+ν_{вy}=\frac{S}{t}+ν_{в}cos(β)=\frac{500}{2}+30×0,866=276 \frac{км}{ч}$ Проекция скорости на ось x
$ ν_{сx} = ν_{вx}=ν_{в}sin(β)=30×sin(\frac{π}{6})=15 \frac{км}{ч}$ Скорость самолета
$ν_{с}=\sqrt{(ν_{сy})^{2}+(ν_{сx})^{2}}=\sqrt{76176+225}=276,41 \frac{км}{ч} $ Находим курс самолета
$ sin(α) = \frac{ν_{сx}}{ν_{с}}=\frac{15}}{276,41}=0.054 $ определяем угол α
$ arcsin(α) = arcsin(0.054)=0.054 рад $ Переводим в градусы
$ α = \frac{0.054×180}{π}=\frac{0.054×180}{3,14}=3,1 град $ Ответ:
$ Скорость самолета 276 \frac{км}{ч}, а курс 3,1° на С_З $ КомментарииОпределите магнитную индукцию в точке, удаленной от одного проводника на растояние r1=6см,а от другого r2=8см.
Данные задачи: По двум длинным параллельным проводам текут токи в одном направлении
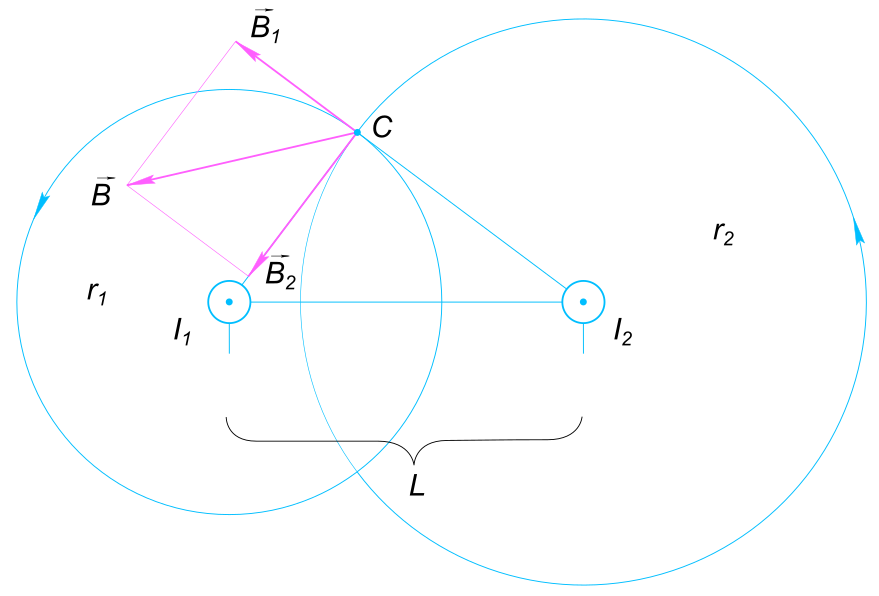
Данные задачи изобразим на рисунке Так как
$ \vect{B}=\vect{B_{1}}+\vect{B_{2}}$ и
$ (L)^{2}=(r_{1})^{2}+(r_{2})^{2}$ То
$ B^{2} = (B_{1})^{2}+(B_{1})^{2}=sqrt{4x} $ Где
$ B_{1} = \frac{μ_{0}I_{1}}{2πr_{1}} $ и
$ B_{2} = \frac{μ_{0}I_{2}}{2πr_{2}} $ Индукция магнитных полей в точке C, создаваемая проводами в отдельности Тогда
$ B = \frac{μ_{0}}{2π}sqrt{\frac{(I_{1})^{2}}{(r_{1})^{2}}+\frac{(I_{2})^{2}}{(r_{2})^{2}}}=\frac{10^{-7}}{2×3,14}×208=33×10^{-7} Тл $ Ответ:
$ Магнитная индукция в точке C равна 33×10^{-7} Тл $ КомментарииКакова скорость шаров после столкновения, если удар абсолютно неупругий? Какая часть энергии пойдет на нагревание шаров?
Данные задачи: Два шара подвешены на двух параллельных нитях
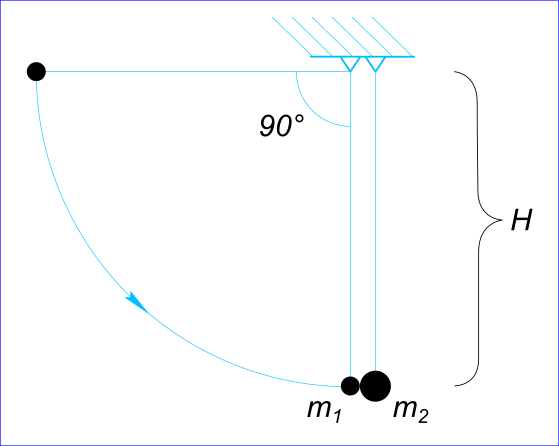
Изобразим на рисунке условия задачи Абсолютно упругим ударом называется такой удар, при котором механическая энергия соударяющихся тел не преобразуется в другие виды энергии. По закону сохранения механической энергии
$ m_{1}gH = \frac{1}{2}m_{1}(v_{1})^{2} $ Откуда находим
$ v_{1}=\sqrt{2gH}=\sqrt{2×9,81×2}=6.264\frac{м}{с} $ Согласно закону сохранения импульса:
$ m_{1}v_{1}+m_{2}v_{2} = m_{1}u_{1}+m_{2}u_{2} $ или
$ m_{1}(v_{1}-u_{1}) = m_{2}(u_{2}-v_{2}) $ Согласно закону сохранения механической энергии:
$ \frac{m_{1}(v_{1})^{2}}{2}+\frac{m_{2}(v_{2})^{2}}{2}=\frac{m_{1}(u_{1})^{2}}{2}+\frac{m_{2}(u_{2})^{2}}{2} $ или
$ m_{1}((v_{1})^{2})-(u_{1})^{2}) = m_{2}((u_{2})^{2})-(v_{2})^{2}) $ Подставив в формулу «разность квадратов» получим
$ m_{1}(v_{1}-u_{1})(v_{1}+u_{1}) = m_{2}(u_{2}-v_{2})(u_{2}+v_{2}) $ Воспользовавшись законом сохранения импульса, находим
$ v_{1}+u_{1} = u_{2}+v_{2} $ Откуда
$ u_{2} = u_{1}+v_{1}-v_{2} $ и
$ u_{1} = u_{2}+v_{2}-v_{1} $ Подставляем в закон сохранения импульса
$ m_{1}(v_{1}-u_{1}) = m_{2}((v_{1}+v_{1}-v_{2})-v_{2}) $ и
$ m_{1}(v_{1}-v_{2}-u_{2}+v_{1}) = m_{2}(u_{2}-v_{2}) $ Раскрываем скобки
$ m_{1}v_{1}-m_{1}u_{1}=m_{2}u_{1}+m_{2}v_{1}-2m_{2}v_{2} $ Откуда
$u_{1}=\frac{2m_{2}v_{2}+(m_{1}-m_{2})v_{1}}{m_{1}+m_{2}}=\frac{(0,2-0,8)×6.26}{0,2+0,8}=-3,76\frac{м}{с}$ Раскрываем скобки
$ m_{1}v_{1}-m_{1}v_{2}-m_{1}u_{2}+m_{1}v_{1}=m_{2}u_{2}-m_{2}v_{2} $ Откуда
$u_{2}=\frac{2m_{1}v_{1}+(m_{2}-m_{1})v_{2}}{m_{2}+m_{1}}=\frac{2×0,2×6,26}{0,8+0,2}=2.51\frac{м}{с}$ Абсолютно неупругий удар характеризуется тем, что кинетическая энергия тел превращается во внутреннюю энергию и после соударения тела либо покоятся, либо движутся с одинаковой скоростью:
$ u = \frac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}=\frac{0,2v_{1}+0,8×0}{0,2+0,8}=0,2×6,26=1.25\frac{м}{с} $ Ответ: Скорость шаров
$ №1 после упругого соударения u_{1}=-3.76\frac{м}{с} $
$ №2 после упругого соударения u_{2}=2.51\frac{м}{с} $
$ после неупругого соударения u=1.25\frac{м}{с} $ КомментарииОпределить внутреннее сопротивление r батареи
Данные задачи: аккумулятор включен в цепь
Расчет кпд батареи выполняется по формуле
$ η = \frac{ε-Ir}{ε} $ Где $Ir $ - потеря напряжения на внутреннем сопротивлении батареи Откуда находим
$ r = \frac{ε(1-η)}{I}=\frac{8(1-0,75)}{2}=1 Ом $ Ответ:
$ Внутреннее сопротивление батареи равно 1 Ом. $ КомментарииОпределить: скорость тела и радиус кривизны траектории
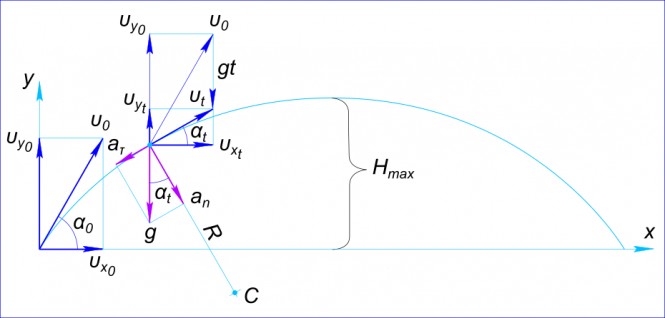
Данные задачи: Тело брошено под углом к горизонту в гравитационном поле Земли
Уравнения описывающие движение тела:
$ x = v_{0}tcos(α) $
$ y = v_{0}tsin(α)-\frac{gt^{2}}{2} $ и
$ v_{y} = v_{0}_{y}-gt=v_{0}sin(α)-gt $ Определяем вертикальную составляющую скорости через 0,5 с после броска
$ v_{y}=v_{0}sin(α)-gt=20×0.866-9,81×0,5=12,415 \frac{м}{с} $ Горизонтальная составляющая неизменна в любой точке траектории
$ v_{x} = v_{0}cos(α)=20×0,5=10 \frac{м}{с} $ Находим результирующую скорость
$ v_{t=τ} = \sqrt{10^{2}+12,415^{2}}=\sqrt{254.13}=15.94 \frac{м}{с} $ Тангенс угла
$ tg(α_{t}) = \frac{v_{y}}{v_{x}}=\frac{12,415}{10}=1,2415 $ Угол
$ α_{t}=arctg(α_{t}) =arctg(1,2415)=0.8927 рад $ Нормальное ускорение
$ a_{n} = \frac{(v_{t})^{2}}{R} $ В то же время
$ a_{n} = gcos(α_{t}) $ Тогда
$ \frac{(v_{t})^{2}}{R} = gcos(α_{t}) $ Откуда
$ R = \frac{(v_{t})^{2}}{gcos(α_{t})}=\frac{254.13}{9,81×0.6273}=41,30 м $ Ответ:
$ v_{t=τ}=15.94 \frac{м}{с}, R= 41,30 м $ КомментарииОпределить силу тока, идущего через R1, если
Данные задачи: замкнутая электрическая цепь
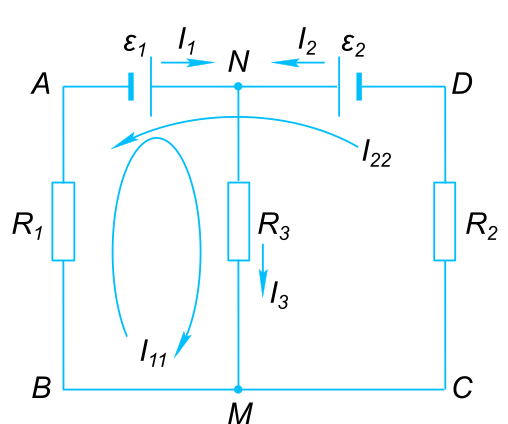
На рисунке изображена замкнутая электрическая цепь. Для нее принято считать, что ток течет от плюса к минусу. В электрическую цепь включены два источника питания. Если источники включены навстречу друг другу (т.е. их полярности противоположны), то их ЭДС вычитаются. 1-й этап. Согласно первому закону Кирхгофа алгебраическая сумма токов в ветвях цепи, соединенных электрическим узлом равна нулю. Для узла N имеем
$ ( I_{1})+(I_{2})+(-I_{3})=0 $ или
$ I_{3}=I_{1}+ I_{2} $ Для решения задачи используем метод контурных токов, в котором на основании второго закона Кирхгоффа выполняем определение значений контурных токов, замыкающихся в независимых контурах. Выберем и рассмотрим два контура ABCD и ABMN, для каждого из них выберем направление обхода. Предположительно определим направление токов в каждом сопротивлении. Для контура ABMN имеем.
$ ε_{1}=I_{3}R_{3}+I_{1}R_{1} $ Для контура ABCD Для контура 2
$ ε_{2}-ε_{1}=I_{2}R_{2}-I_{3}R_{3} $ 2-й этап. Из уравнения (1)
$ I_{3}=\frac{ε_{1}-I_{1}R_{1}}{R_{3}} $ А из уравнения (2)
$ I_{2}=\frac{ε_{2}-ε_{1}+I_{1}R_{1}}{R_{2}} $ Тогда
$ I_{1}=I_{3}-I_{2}=\frac{ε_{1}-I_{1}R_{1}}{R_{3}}-\frac{ε_{2}-ε_{1}+I_{1}R_{1}}{R_{2}} $ Решаем уравнение относительно I_{1}
$I_{1}R_{3}R_{1}=ε_{1}R_{2}-I_{1}R_{1}R_{2}-ε_{2}R_{3}+ε_{1}R_{3}-I_{1}R_{1}R_{3}$
$I_{1}(R_{3}R_{2}+R_{1}R_{2}+R_{1}R_{3})=ε_{1}R_{2}-ε_{2}R_{3}+ε_{1}R_{3}$ или окончательно
$I_{1}=\frac{ε_{1}R_{2}-ε_{2}R_{3}+ε_{1}R_{3}}{R_{3}R_{2}+R_{1}R_{2}+R_{1}R_{3}}=\frac{1,4×1-2×3+1,4×3}{1×3+5×1+5×3}=-0,017 А$ Знак «минус» означает, что мы ошиблись в выборе направления тока I_{1}. Ответ:
$ Сила тока идущего через R_{1} составляет -0.017 А $ КомментарииВо сколько раз увеличивается сопротивление лампы при нагреве?
Данные задачи: вольфрамовая нить электролампы в процессе своей работы нагревается
Зависимость сопротивления проводника от его нагрева определяется выражением
$ R_t= R_{t_0}(1+α∆t) $ Где:
$ R_t - конечное и R_{t_0} - начальное сопротивления лампы $ Откуда
$ \frac{R_t}{R_{t_0}}= (1+α∆t)=(1+0,005×2400)=13 $ Ответ:
$ сопротивление лампы увеличится в 13 раз $ КомментарииГруз массой 200 кг нужно повесить на кронштейне, у которого один из стержней горизонтальный
Данные задачи: кронштейн из двух стержней, к нему подвешен груз
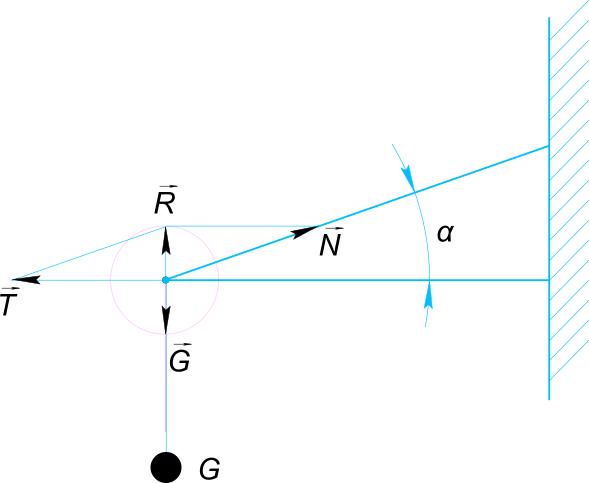
Составляем схему, полагая что усилия реакций направлены вдоль стержней Груз находится в состоянии покоя, поэтому воспользуемся для решения задачи Первым законом Ньютона - тело движется прямолинейно и равномерно, или находится в состоянии покоя, если результирующая всех действующих на тело сил равна нулю
$ 0 = →G + →N + →T $ Учитывая, что
$ R = G $ находим
$ N = \frac{G}{sinα} = \frac{200×9,81}{0.342} = 5736.84 Н $ и
$ T = \frac{G}{tgα} = \frac{200×9,81}{0.364} = 5390.11 Н $ Ответ:
$ Реакция в горизонтальном стержне равна 5390.11 Н $ и
$ Реакция в наклоненном стержне равна 5736.84 Н $ КомментарииНайти жёсткость пружины
Пример текста Данные задачи: Брусок с помощью горизонтальной пружины тянут равномерно по доске, расположенной горизонтально
Анализируем условие задачи: - брусок движется равномерно; - на брусок действует сила трения и сила натяжения пружины. Для решения задачи применяем Первый закон Ньютона - тело движется прямолинейно и равномерно, или находится в состоянии покоя, если результирующая всех действующих на тело сил равна нулю. Составляем уравнение
$ Fпр - Fтр = sD - fmg =0 $ Откуда находим жесткость пружины
$ D = \frac{fmg}{s} = \frac{0,25×3×9,81}{0,05} = 147,15 \frac{Н}{м} $ Ответ: жесткость пружины равна
$ D = 147,15 \frac{Н}{м} $ КомментарииОпределить кинетическую энергию цилиндра и время остановки.
Пример текста Данные задачи: Сплошной цилиндр массой катится без скольжения с постоянной скоростью
Анализируем условие задачи: Цилиндр имеет два состояния - катится и остановился; Остановка цилиндра наступает в результате приложения к нему силы F=50 Н; Кинетическая энергия цилиндра растрачивается на преодоление работы силы F. Составляем уравнение
$ \frac{1}{2}mv^2 - FS = 0 $ Где S - путь, пройденный цилиндром до его остановки Кинетическая энергия цилиндра до момента приложения силы F
$ \frac{1}{2}mv^2 = \frac{1}{2}×10×10^2 = 500 дж $ Составляем уравнение
$ F = ma $ Где a - ускорение вызываемое силой F Откуда
$ a = \frac{F}{m} $ Составляем уравнение пути пройденного цилиндром
$ S = \frac{1}{2F}mv^2 $ Составляем уравнение пути пройденного цилиндром
$ S = at^2 $ Тогда
$ t^2 = \frac{1}{2Fa}mv^2 $ или
$ t = sqrt{\frac{1}{2F}mv^2\frac{m}{F}} = \frac{mv}{F}sqrt{\frac{1}{2}} = 1,77 с $ Ответ:
$ Кинетическая энергия цилиндра 500 дж, t = 1,77 с $ КомментарииОпределить ускорения g
Определить ускорение g, если расстояния между метками оказались равными 23, 40, 56, 74, 91, 110, 126 и 143 мм. Измерения показали, что число оборотов двигателя равно 1440 об/мин. Подсчитываем количество меток
$ Z = 8 $ Тогда количество оборотов двигателя
$ N = Z - 1 = 8 - 1 = 7 об $ Движение тела двигающегося с постоянным ускорением описывает уравнение
$ h = \frac{gt^2}{2} $ Путь пройденный от первой метки до последней
$ h = 143 - 23 = 120 мм = 0,12 м $ Приводим к СИ обороты двигателя
$ n = \frac{1440}{60} = 24\frac{об}{с} $ Время в пути от первой метки до последней
$ t = \frac{N}{n} = \frac{7}{24} с $ Тогда ускорение равно
$ g = \frac{2h}{\frac{N^2}{n^2}} = \frac{2×0,12×576}{49} = 2,82 \frac{м}{с^2} $ Ответ:
$ Ускорение с которым падает цилиндр равно 2,82 \frac{м}{с^2} $ КомментарииДве материальные точки движутся согласно уравнениям
Дано:
Закон движения M
$ x = A1 + B1t + C1 t^2 $ Закон движения N
$ x^2 = A2 + C2 t^2 $ где:
таблица 3
Чтобы получить закон изменения скорости берем производную от закона движения M
$ U = (10 + 32 t - 3 t^2)' = 32 - 6t $ Чтобы получить закон изменения скорости берем производную от закона движения N
$ V = (sqrt(5 + 5 t^2))' = \frac{5t}{sqrt(5t^2+5)} $ Составляем уравнение
$ 32 - 6t = \frac{5t}{sqrt(5t^2+5)} $ 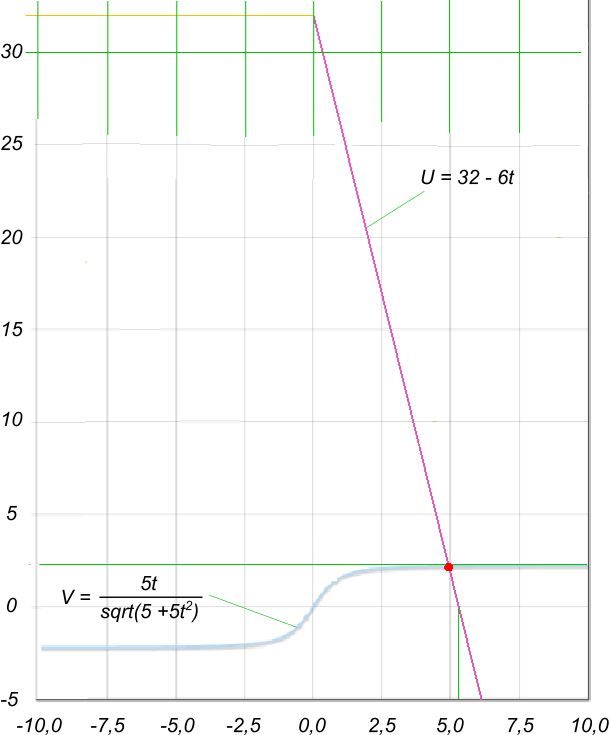
На рисунке представлены графики скоростей. При to = 4,97 с U = V = 2,18 Чтобы получить закон изменения ускорения берем производную от закона скорости M
$ a = (32-6t)' = - 6 $ Ускорение точки M постоянно, следовательно
$ ao = - 6 \frac{м}{с^2} $ Чтобы получить закон изменения ускорения берем производную от закона скорости N
$ go = \frac{sqrt(5)}{sqrt(t^2+1)} (1 - \frac{t^2}{t^2+1}) = 0.017 \frac{м}{с^2} $ КомментарииНайдите работу силы трения.
Дано:
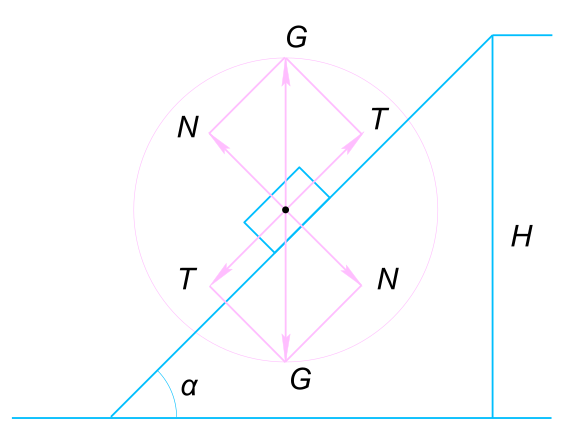
Изображаем на рисунке условия задачи Составляем уравнение для работы силы трения
$ W = N f S = f S G cos α $ Составляем уравнение
$ sin α = \frac{H}{S} $ Откуда находим путь проделанный телом по наклонной плоскости
$ S = \frac{H}{sin α} $ Тогда работа силы трения
$ W = f \frac{H}{sin α} G cos α = \frac{fGH}{tg α} = \frac{0,2 × 0,5 × 9,81 × 7}{1} = 6,87 Дж $ КомментарииОпределить вес груза и силу натяжения нити
Система находится в состоянии покоя. Поэтому для решения задачи применяем Первый закон Ньютона - тело движется прямолинейно и равномерно, или находится в состоянии покоя, если результирующая всех действующих на тело сил равна нулю. 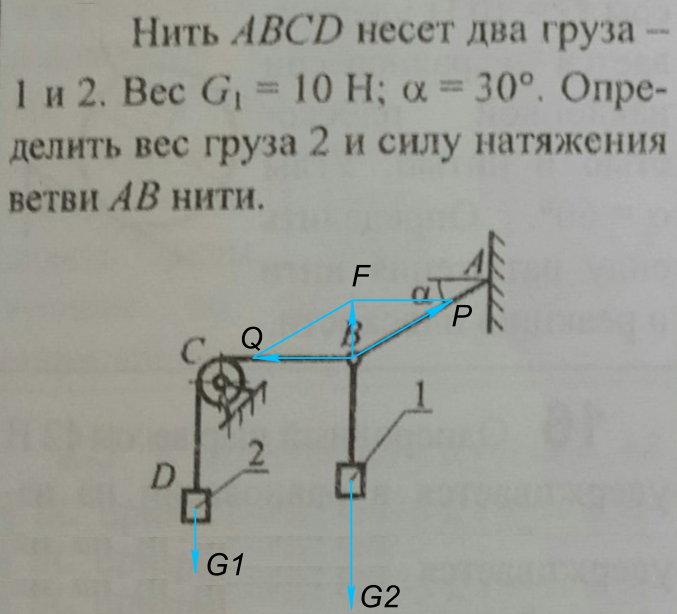
Строим равнодействующую всех сил приложенных к точке B Дано:
Составляем уравнение
$ tg α = \frac{F}{Q} $ Откуда находим натяжение нити на участке BC
$ Q = \frac{F}{tg α} = \frac{10}{0.577} = 17.331 Н $ Ответ: так как натяжение нити Q на участке BC равно весу груза 2, то вес груза 2
$ G2 = Q = 17.331 Н $ Составляем уравнение
$ sin α = \frac{F}{P} $ Откуда находим натяжение нити на участке BA
$ P = \frac{F}{sin α} = \frac{10}{0,5} = 20 Н $ КомментарииАвтомобиль движется с постоянной скоростью v=72 км /ч. У подножия горы водитель выключил мотор. Уклон горы 5 м на 1 км пути.
Данные задачи:
Кинетическая энергия автомобиля превращается в потенциальную за вычетом работы совершаемой силой трения
$ \frac{1}{2}mU^2 - fmgS= mgh $ Высоту подъема автомобиля выражаем через уклон горы и путь пройденный автомобилем
$ h = iS $ Подставив в составленное уравнение получаем
$ \frac{1}{2}U^2 = (f + i)gS $ Откуда находим
$ S = \frac{\frac{1}{2}U^2}{(f + i)g} = \frac{U^2}{2(f + i)g} $ Вычисляем скорость автомобиля в метрах в секунду
$ U = \frac{72 ×10^3}{3,6 × 10^3} = 20 \frac{м}{с} $ и тогда находим
$ S = \frac{20^2}{2(0,02 + 0,005) × 9,81} = 815.49 м $ Ответ:
Автомобиль преодолеет расстояние равное 815.49 м КомментарииНайти величину бокового смещения луча
Дано: H=6 см; α=60°=π/3; $n_{возд}$=1; $n_{ст}$=1,57 h=? 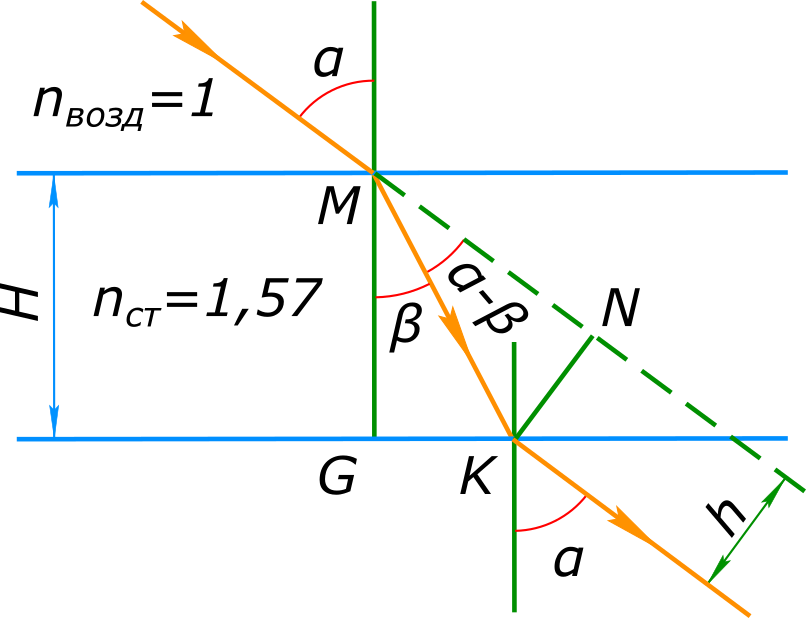
Изобразим графически условие задачи Решение: Согласно закону преломления света $\frac{sinα}{sinβ}=\frac{n_{ст}}{n_{возд}}$, откуда $sinβ=\frac{n_{возд}sinα}{n_{ст}}=\frac{1×0,866}{1,57}$=0,5516, откуда $β=arcsin0,5516$=0,5843 Из треугольника MGK находим $cosβ=\frac{MG}{MK}$, откуда $MK=\frac{MG}{cosβ}$ Из треугольника MKN находим $sin(α-β)=\frac{KN}{MK}$, откуда $h=KN=MKsin(α-β)=\frac{MGsin(α-β)}{cosβ}=\frac{6sin(\frac{π}{3}-0,5843)}{cos0,5843}=\frac{6×0,4465}{0,834}$=3,2 см. Ответ: величина бокового смещения луча составит 3,2 см. КомментарииПри каком значении угла падения луч, отраженный от поверхности воды будет перпендикулярен к преломленному лучу?
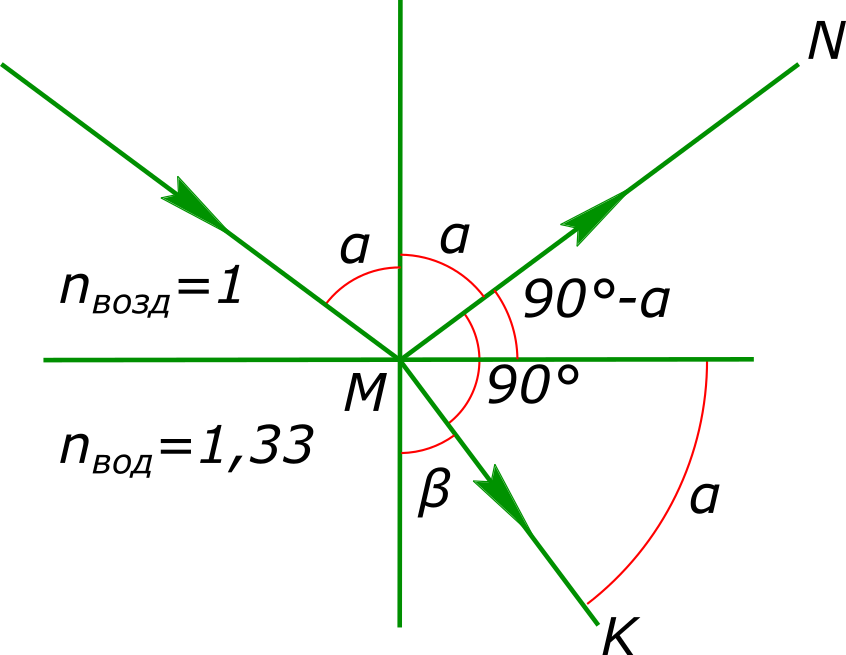
Изобразим условия задачи на рисунке Данные задачи: луч света падает на поверхность воды
Согласно закону преломления света
$\frac{sinα}{sinβ}=\frac{n_{вод}}{n_{возд}}$ из рисунка находим
$ β=90°- α $ тогда
$sinβ=sin(90°-α)=cosα$ подставляем в уравнение
$\frac{sinα}{cosα}=\frac{n_{вод}}{n_{возд}}$ вычисляем
$ tgα=1,33 $ получим значение угла падения
$ α=arctgα=arctg1,33=0,926 рад $ радианную меру переведем в градусную
$ α=\frac{0,926×180°}{3,14}=53° $ Ответ: При значении угла падения 53°.
$ При значении угла падения 53° $ КомментарииКакой угол наименьшего отклонения даст призма в воде?
Дано: трехгранная призма в двух средах - водзухе и воде
Изображаем графически условие задачи 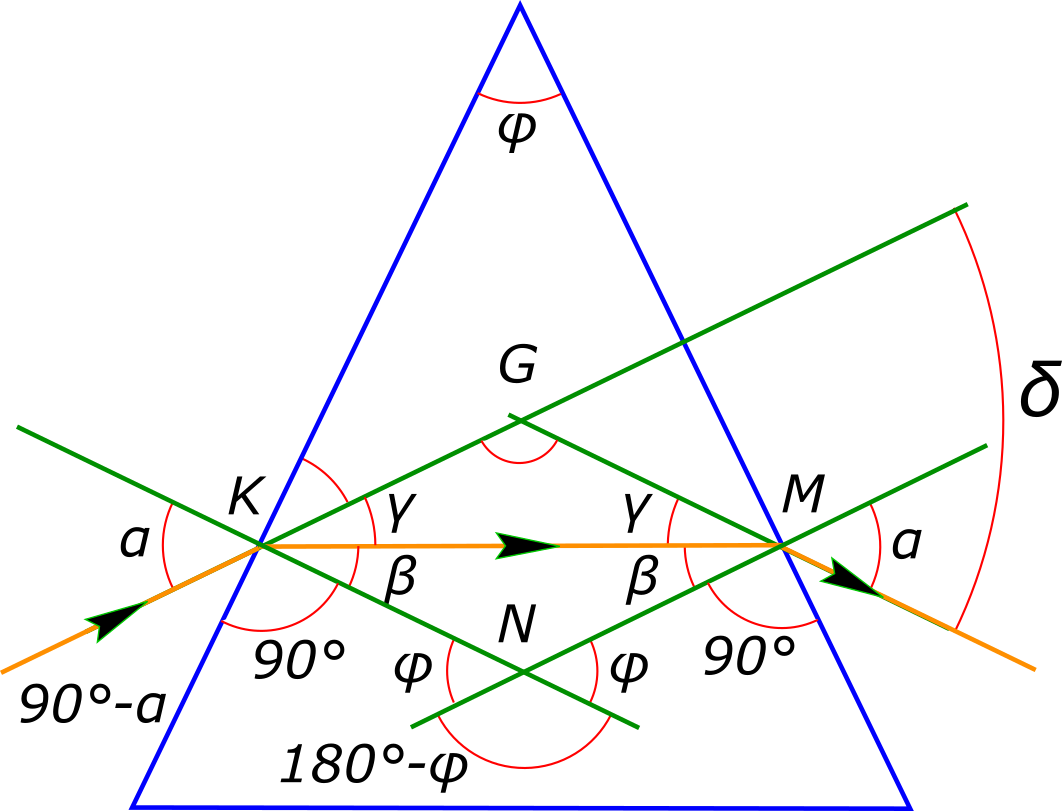
рисунок 1 Рассматривая треугольник KMN можем записать
$ N+2β=180°$ , где $N=180°-φ$, откуда $φ=2β $ Рассматривая треугольник GKM можем записать
$ G=180-2γ=180°-δ$, откуда $δ=2γ $ и
$ α=β+γ=\frac{φ}{2}+\frac{δ}{2} $ Угол наименьшего отклонения призмы в воздухе
$ α_{возд}=\frac{60°}{2}+\frac{37°}{2}=48,5° $ Находим значение функции
$ sinα_{возд}=sin(\frac{3,14×48,5°}{180°})=sin0,8465=0,749 $ Закон преломления света для призмы в воздухе (1)
$ \frac{sinα_{возд}}{sinβ}=\frac{n}{n_{возд}} $ Закон преломления света для призмы в воде (2)
$ \frac{sinα_{вод}}{sinβ}=\frac{n}{n_{вод}} $ Разделив первое уравнение на второе получим
$ \frac{sinα_{возд}}{sinα_{вод}}=\frac{n_{вод}}{n_{возд}} $ Откуда
$ sinα_{вод}=\frac{sinα_{возд}}{\frac{n_{вод}}{n_{возд}}}=0,749×\frac{1}{1,33}=0,563 $ Угол наименьшего отклонения призмы в воде
$ α_{вод}=arcsinα_{вод}=arcsin0,563=0,598 $ переводим радианы в градусы
$ α_{вод}=\frac{0,598×180°}{3,14}=34,3° $ Находим
$ δ=2α-φ $ тогда
$ δ_{вод}=2α_{вод}-φ=2×34,3°-60°=8,6° $ Ответ:
$ в воде угол наим. отклонения призмы составит 8,6° $ КомментарииНа каком расстоянии друг от друга были поезда?
Данные задачи: два поезда двигаются навстречу друг другу
Для равномерного поступательного движения
$u=\frac{S}{t}$, откуда
$S=ut$ Тогда применительно к задаче можем составить уравнения:
$S_{1}=427-(u_{А}+u_{Б})t_{1}=427-(52+63)×2=197 [км]$ и
$S_{2}=427-(u_{А}+u_{Б})t_{2}=427-(52+63)×3=82 [км]$ Ответ:
$через 2 ч. расст. между поезд. 197 км, а через 3 ч. 82 км$ КомментарииКак далеко от берега находилась лодка?
Данные задачи: волна дошла до берега
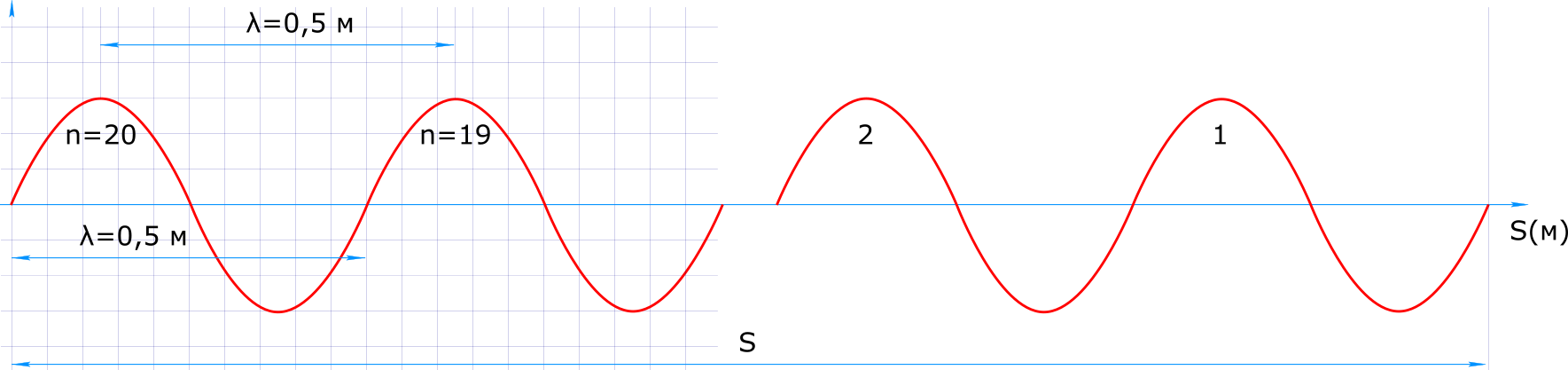
Изобразим условия задачи в рисунке время за которое волна проходит путь равный длине волны
$ T=\frac{t}{n}=\frac{20}{20}=1 [с] $ в соответствии с формулой равномерного поступательного движения скорость распространения волны
$ c=\frac{λ}{T}=λf $ где
$ f=\frac{1}{T}=\frac{1}{1}=1 [с^{-1}] $ тогда
$ λ=cT=\frac{c}{f} $ Принимая все это во внимание
$ S=cτ=fλτ=1×0,5×50=25 [м] $ Ответ:
$ лодка находилась от берега на расстоянии 25 м $ КомментарииВыпадет ли роса?
Данные задачи:
Справочные данные
$Решение$
Ответ: утром относительная влажность воздуха не превысила 100%, значит роса не выпадет. КомментарииКакая масса воды выкипит за 20 минут
Дано СИ: $R=160$ [Ом], $m=0,5$ [кг], $T_1=20$ [°C], $T_2=100$ [°C], $U=220$ [В], $τ=20$ [Мин] = 20×60 = 1200 [с], $η=0,8$ Из справочника берем: $c=4187$ [$\frac{Дж}{кг×К}$], $r=2260×10^3$ [$\frac{Дж}{кг}$] Нагрев воды от 20° до 100° или через какое время вода закипит: $W=\frac{ηU^2τ}{R}$=$cm(T_2-T_1)$, отсюда $τ_нагр=\frac{Rcm(T_2-T_1)}{ηU^2}$=$\frac{160×4187×0,5(100-80)}{0,8×220^2}$=692 [с] Тогда время для парообразования: $τ_пар=τ-τ_нагр$ = 1200-692 = 508 [с], и энергия на парообразование $W_пар=\frac{ητU^2}{R}=\frac{0,8×508×220^2}{160}$ = 122936 [Дж] Масса пара $m=\frac{W_пар}{r}=\frac{122936}{2260×10^3}$ = 0,054 [кг] Ответ: выкипит за 20 минут работы кипятильника 0,054 кг воды. КомментарииНайти молярную массу воздуха
Согласно уравнению Менделеева-Клайпейрона: $pV=RT\frac{m}{μ}$, откуда $μ=\frac{mRT}{pV}$ $\frac{m}{V}=ρ$, отсюда $μ=\frac{ρRT}{p}=\frac{1,225×8,31×288}{101325}$=0,0289 $\frac{кг}{моль}$ Ответ: молярная масса воздуха при нормальных условиях равна 0,0289 кг/моль КомментарииНайти работу силы сопротивления воздуха
Данные задачи: парашютист пролетел не раскрывая парашюта
Составляем уравнение силы тяжести и силы сопротивления воздух
$W=FS=maS=m(g-b)h$ откуда результируещее ускорение от силы тяжести и от силы сопр.воздуха
$a=g-b$ в то же время
$S=(g-b)t^2=200 м$ и
$v_{200}=(g-b)t=50 м/с$ время падения
$t=\frac{S}{v_{200}}=\frac{200}{50}=4 с$ Ускорение от силы сопротивления воздуха
$b=\frac{v_{200}-gt}{t}=\frac{50-9,81×4}{4}=2,69\frac{м}{с^2}$ Работа силы сопротивления воздуха
$W_сопр=mbS=4×2,69×200=2152 Дж$ Ответ:
$ Работа силы сопр. воздуха равна 2152 Дж. $ КомментарииНайти работу силы тяжести
$W=FS=GS=mgh$ $v_2=gt_2$ $v_1=gt_1$ $\frac{v_2}{v_1}=\frac{t_2}{t_1}$ $t_1=\frac{v_1}{g}=\frac{2}{10}$=0,2 c $W_2=mggt_2^2$ $W_1=mggt_1^2=4×10^2×(\frac{2}{10})^2$=16 Дж $\frac{W_2}{W_1}=\frac{t_2^2}{t_1^2}=(\frac{v_2}{v_1})^2=(\frac{8_2}{2_1})^2$=16 $W_2=16W_1$=16×16=256 Дж $W=W_2-W_1$=256-16=240 Дж Ответ: работа силы тяжести равна 240 Дж. Комментарии
|
Записать новую задачу Все задачи Все темы Все физики |


Комментарии