Все решения физика @NICKРешить задание ЕГЭ
Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S = 100 см2. В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой T. Если нить перерезать, то шар всплывёт, а уровень воды изменится на h = 5 см. Найдите силу натяжения нити T. Запишем данные задачи таблица 1
Решение: Упростим условие задачи: Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S = 100 см2, наполненного водой. Если погружать в воду шар, плавающий на поверхности, до того момента когда он окажется полностью погруженным в жидкость, посредством натяжения нити, то уровень воды в сосуде поднимется на h = 5 см. Найдите силу натяжения нити T. На шар действуют сила натяжения нити и сила Архимедова. Шар находится в покое, значит согласно первому закону Ньютона силы приложенные к нему уравновешивают друг друга
$ T=F_{Арх}=ρghS=1000×10×0,05×0,01=5 Н $ где плотность воды —
$ ρ $ Ответ: сила натяжения нити равна 5 Н. Решить задание ЕГЭ
Деревянный шар привязан нитью ко дну цилиндрического сосуда с площадью дна S = 100 см2. В сосуд наливают воду так, что шар полностью погружается в жидкость, при этом нить натягивается и действует на шар с силой T. Если нить перерезать, то шар всплывёт, а уровень воды изменится на h = 5 см. Найдите силу натяжения нити T. Запишем данные задачи таблица 1
Решение До перерезания нити на дно действуют сила давления столба жидкости и сила натяжения нити
$ F_{до}=ρgHS - T $ После перерезания нити на дно действуют сила давления столба жидкости
$ F_{после}=ρg(H-h)S $ Поскольку масса системы вода-шар постоянна, ее вес в равновесных состояниях один и тот же, приравниваем эти силы
$ ρgHS - T=ρg(H-h)S $ Откуда
$ T=ρg(HS-(H-h)S)=ρghS=1000×10×0,05×0,01=5 Н $ Ответ: сила натяжения нити равна 5 Н. КомментарииКакую скорость должен иметь искусственный спутник?
Решение: Центростремительная сила при движении спутника по круговой орбите
$ ma_{ц} = m\frac{υ^{2}}{R} $ С другой стороны, гравитационная сила притяжения к земле
$ F_{гр} = mg = m\frac{GM_{з}}{(R_{з}+h)^{2}} $ Имеем равномерное движение по окружности, поэтому
$ m\frac{υ^{2}}{R_{з}+h} = m\frac{GM_{з}}{(R_{з}+h)^{2}} $ Тогда
$ υ^{2}} =\frac{GM_{з}}{(R_{з}+h)} $ Откуда
$ υ=\sqrt{\frac{GM_{З}}{R_{З}+h}} $ Учитывая что: масса Земли
$ M_{З} = 6×10^{24} кг $ И Гравитационная постоянная
$ G = 6,67×10^{-11} \frac{Н×м^{2}}{кг^{2}} $ Получаем
$ υ=\sqrt{\frac{6,67×10^{-11}×6×10^{24}}{6400×10^{3}+600×10^{3}}}= $
$ = 7561 \frac{м}{с} $ Ответ: скорость спутника $7561 \frac{м}{с}$ КомментарииКакую скорость должен иметь искусственный спутник?
Какую скорость должен иметь искусственный спутник, чтобы обращаться по круговой орбите на высоте 600 км над поверхностью Земли? Каков период его обращения? Радиус Земли 6400 км. Запишем данные задачи таблица 1
КомментарииОпределить КПД машины и температуру нагревателя, если температура холодильника 17°C
В идеальной тепловой машине Карно за счет каждого килоджоуля энергии, получаемой от нагревателя, Совершается работа 300 Дж. Определить КПД машины и температуру нагревателя, если температура холодильника 17°C. Запишем данные задачи таблица 1
Решение КПД тепловой машины равен
$ η = \frac{A}{Q_{х}+A}=\frac{300}{1000+300}=0,23 $ С другой стороны
$ η =1 - \frac{T_{x}}{T_{н}} $ Откуда
$ T_{н}=\frac{T_{x}}{1 - η}=\frac{T_{x}}{1 - \frac{A}{Q_{х}+A}}= $
$ =\frac{T_{x}(Q_{х}+A)}{Q_{х}+A-A}=T_{x}(1+\frac{A}{Q_{х}})= $
$ =290(1 + \frac{300}{1000})=290+87=377 K $ Ответ: КПД машины равен 0,23 и температура нагревателя 87°C. КомментарииКаково значение мощности?
P - мощность , отдаваемая электрической батареей, определяется по формуле формула 1,
$ P=\frac{E^{2}R}{(R+r)^{2}} $ E = const, r = const, R - var Задавая различные значения переменной R можем построить график функции P: R=0; P=0; R=∞; P=0; 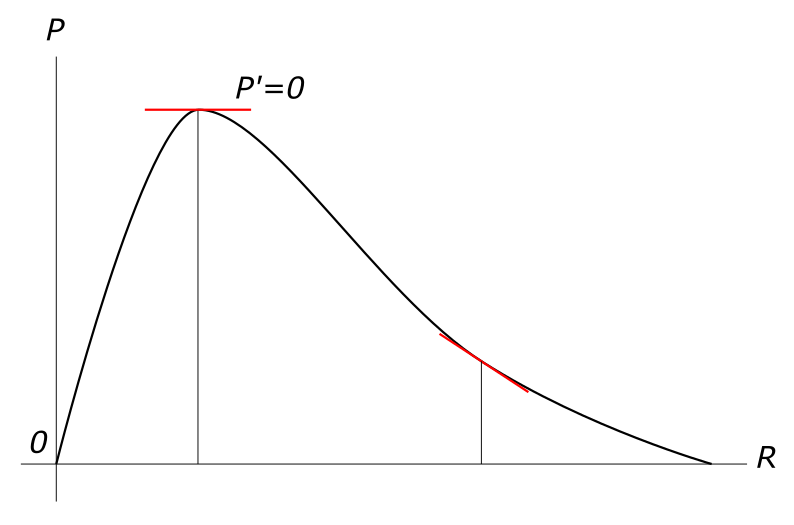
Находим экстремум функции P
$ P' = \frac{E^{2}R}{(R+r)^{4}}(-2R-2r)+\frac{E^{2}}{(R+r)^{2}}=0 $ Откуда находим корень этого уравнения
$ R_{1} = r $ Тогда
$ P = \frac{E^{2}r}{(r+r)^{2}}=\frac{E^{2}r}{4r^{2}}=\frac{E^{2}}{4r} $ КомментарииНайти силу тока протекающего через лампу
К двум батареям,соединенным параллельно, подключили электролампу, сопротивление которой 0,5 ом. э.д.с. батареи ε1 = 12 В, ε2-=10 В и их внутреннее сопротивление r1=r2=1 Ом. Найти ток протекающий через лампу. 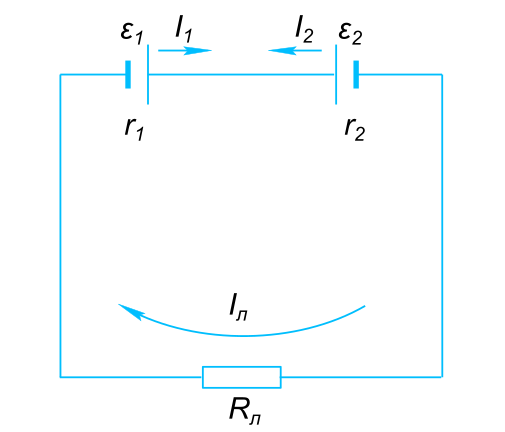
К двум батареям,соединенным параллельно, подключили электролампу таблица 1
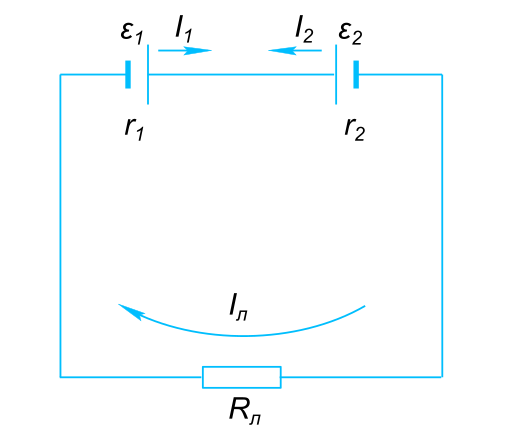
Электрическая схема подключения двух батарей и лампы Напряжение в цепи равно сумме падений напряжений на приборах включенных в цепь
$ |\vect{U_{1}}+\vect{U_{2}}| = |(r_{1}+r_{2}+R_{л})\vect{I_{л}}| $ Или в скалярной форме
$ U_{1}-U_{2} = (r_{1}+r_{2}+R_{л})I_{л} $ Откуда находим
$ I_{л} = \frac{U_{1}-U_{2}}{r_{1}+r_{2}+R_{л}} = \frac{12-10}{1+1+0,5}= 0,8 А $ Ответ: Сила тока в лампе
$ I_{л} = 0,8 А $ КомментарииНайдите модуль вектора напряженности поля в точке
Потенциал поля создаваемого некоторой системой зарядов, зависит от координат по закону φ=a(x^2+y^2)-bz^2, где a=5 В/м^2, b=10 В/м^2. Найдите модуль вектора напряженности поля в точке с координатами (1; 1; 1). Координаты указаны в метрах. Вектор напряженности электрического поля в каждой точке силовой линии направлен по касательной к ней
$ |\vect{E}| = φ' = a(2x+2y)-b2z =5(2×1+2×1)-10×2×1=0 $ Ответ:
$ |\vect{E}|=0 $ КомментарииНайдите заряд на конденсаторе
Электрическая энергия заряженного конденсатора емкостью 2пФ составляет 0,1 мДж. Найдите заряд на конденсаторе. таблица 1
Потенциальная энергия заряженного конденсатора определяется по формуле
$ W_{p} = \frac{q}{2C} $ Откуда находим заряд на конденсаторе
$ q = 2CW_{p}=2×2×10^{-12}×0,1×10^{6}=0,4×10^{-6} Кл $ Ответ: Заряд на конденсаторе равен
$ 0,4×10^{-6} Кл $ КомментарииНайдите во сколько раз у этого конденсатора меньше напряженность электрического поля
Два плоских конденсатора заряжены одинаковыми зарядами. У одного конденсатора емкость в два раза больше, хотя расстояние между пластинами тоже в два раза больше. Найдите во сколько раз у этого конденсатора меньше напряженность электрического поля. Два плоских конденсатора заряжены одинаковыми зарядами
Емкость конденсатора определяется по формуле
$ C = \frac{q}{U} $ Откуда
$ U = \frac{q}{C} $ Напряжение на конденсаторе
$ U = ED $ Тогда напряженность электрического поля
$ E = \frac{\frac{q}{C}}{d} $ Для первого конденсатора
$ E_{1} = \frac{\frac{q}{C_{1}}}{d_{1}} $ Для второго конденсатора
$ E_{2} = \frac{\frac{q}{C_{2}}}{d_{2}}=\frac{\frac{q}{\frac{1}{2}C_{1}}}{\frac{1}{2}d_{1}}=\frac{q}{\frac{1}{2}C_{1}\frac{1}{2}d_{1}} $ Находим соотношение
$ \frac{E_{1}}{E_{2}} = \frac{\frac{\frac{q}{C_{1}}}{d_{1}}}{\frac{\frac{q}{\frac{1}{2}C_{1}}}{\frac{1}{2}d_{1}}}=\frac{q}{C_{1}d_{1}}}\frac{\frac{1}{2}C_{1}\frac{1}{2}d_{1}}{q}=\frac{1}{4} $ Откуда
$ 4E_{1} = E_{2} $ Ответ:
$ В 4 раза $ КомментарииВо сколько раз медленнее нагреет воду до кипения нагреватель
Найдите, во сколько раз медленнее нагреет воду до кипения нагреватель, состоящий из четырех последовательно соединенных спиралей, чем нагреватель, состоящий из четырех таких же спиралей, но соединенных параллельно. Данные задачи: замкнутая электрическая цепь
Мощность в замкнутой электрической цепи определяется по формуле
$ P = UI=U\frac{U}{R}=\frac{U^2}{R} $ где
$ R - сопротивление электрической цепи $ Для нагревателя с последовательным включением четырех спиралей сопротивление электрической цепи
$ R_{посл} = R_{1}+R_{2}+R_{3}+R_{4}=4R $ Тогда
$ P_{посл} = \frac{U^{2}}{R_{посл}}=\frac{U^{2}}{4R} $ Для нагревателя с параллельным включением четырех спиралей сопротивление электрической цепи
$ R_{пар} = \frac{\frac{R_{1}R_{2}R_{3}R_{4}}{(R_{1}+R_{2})(R_{3}+R_{4})}}{\frac{R_{1}R_{2}}{R_{1}+R_{2}}+\frac{R_{3}R_{4}}{R_{3}+R_{4}}}=\frac{\frac{R^{4}}{4R^{2}}}{\frac{R^{2}}{2R}+\frac{R^{2}}{2R}}=\frac{R}{4} $ и окончательно
$ P_{пар} = \frac{U^{2}}{R_{пар}}=\frac{U^{2}}{\frac{R}{4}}=\frac{4U^{2}}{R}} $ Тогда
$ \frac{P_{посл}}{P_{пар}}=\frac{\frac{U^{2}}{4R}}{\frac{4U^{2}}{R}}=\frac{1}{16} $ Откуда находим
$ 16P_{посл} = P_{пар} $ Ответ:
$ В 16 раза медленнее $ КомментарииНайти силу тяги вертолета и силу, действующую со стороны груза на прицепной механизм вертолета
Пример текста Данные задачи: Вертолет поднимает груз на тросе
Рассматриваем силы действующие на поднимаемый вертикально вверх вертолетом груз:
$ \vect{F_{m.гр}}=m_{гр}\vect{g} - сила тяжести $ и
$ \vect{F_{тр}} - сила натяжения троса $ Составляем уравнение движения груза
$ m_{гр}a = F_{тр}-F_{m.гр}=F_{тр}-m_{гр}g $ Откуда находим силу натяжения троса
$ F_{тр}=m_{гр}(g+a)=10000×(10+1)=11000 Н $ Рассматриваем силы действующие на поднимающиеся вертикально вверх вертолет и груз:
$ \vect{F_{т}} = (m_{в}+m_{гр})\vect{g} - сила тяжести $ и
$ \vect{F_{в}} - сила тяги вертолета $ Составляем уравнение движения вертолета и груза
$ (m_{в}+m_{гр})a = F_{в}-F_{т} $ Откуда находим силу тяги вертолета
$F_{в}=(m_{в}+m_{гр})(g+a)=40000(10+1)=440000 Н $ Ответ:
$ Сила, действующая со стороны груза 11000 Н $ и
$ сила тяги вертолета 440000 Н $ КомментарииС какой скоростью вытекает газ их трубы
Пример текста Данные задачи: по цилиндрической трубе истекает горячий газ
Запишем уравнение Менделеева-Клайпейрона для двух состояний газа
$ P_{1}V_{1} = \frac{m}{μ}RT_{1} $ и
$ P_{2}V_{2} = \frac{m}{μ}RT_{2} $ Объем газа ежесекундно протекающего через сечение трубы
$ V = υS $ где
$ S - площадь сечения трубы $ Тогда
$ V_{1} = υ_{1}S $ и
$ V_{2} = υ_{2}S $ Подставляем в исходные уравнения и делим первое на второе
$ \frac{P_{1}υ_{1}}{P_{2}υ_{2}} = \frac{T_{1}}{T_{2}} $ По условию
$ P_{1}=nP_{2} $ Тогда
$ υ_{2} = nυ_{1}\frac{T_{2}}{T_{1}}=1,5×5\frac{573}{973}=4,4 \frac{м}{с} $ Ответ:
$ Скорость истечения газа на выходе 4,4 \frac{м}{с} $ КомментарииОпределить среднюю квадратичную скорость молекул газа
Данные задачи: газ находится под давлением
Средняя квадратичная скорость
$ υ = \sqrt{\frac{3RT}{μ}} $ Уравнение Менделеева-Клайпейрона
$ PV = \frac{m}{μ}RT $ Или
$ P =ρ\frac{RT}{μ} $ Откуда находим
$ \frac{P}{ρ} = \frac{RT}{μ} $ и тогда
$ υ = \sqrt{3\frac{RT}{μ}}=\sqrt{3\frac{P}{ρ}}=\sqrt{3\frac{2×1,01×10^{5}}{1,2}}=711 \frac{м}{с} $ Ответ:
$ Средняя квадратичная скорость молекул газа 711 \frac{м}{с} $ КомментарииКакое число молекул воды содержится в сосуде? Найти массу молекулы и оценить ее размер.
Данные задачи: Вода в сосуде
Число молекул можно найти, если определить число молей воды в занимаемом ею объеме
$ N = N_{A}ν $ Зная химическую формулу воды
$ H_{2}O $ с помощью периодической системы элементов Д.И. Менделеева находим ее молярную массу
$ μ = (1×2+16)×10^{-3}=18×10^{-3}\frac{кг}{моль} $ Число молей
$ ν = \frac{m}{μ} $ Массу вещества находим
$ m = ρV $ $ρ - плотность воды$ узнаем из таблиц физических величин, ее значение заданное при определенной температуре Откуда находим число молекул
$ N = N_{A}\frac{ρV}{μ}=6,02×10^{23}\frac{1000×10^{-5}}{18×10^{-3}}=3,34×10^{23} молекул $ Масса одной молекулы
$ m_{0} = \frac{μ}{N_{A}}=\frac{18×10^{-3}}{6,02×10^{23}}=2,99×10^{-26} кг $ Чтобы оценить размер молекулы d, сделаем допущение: молекулы плотно прилегают друг к другу и образуют кубическую ячейку. Тогда объем молекулы
$ V_{0} = d^{3} $, а
$ d = \sqrt{V_{0}} $ С другой стороны, объем занимаемый одной молекулой, можно найти зная объем воды и число молекул в этом объеме
$ V_{0} = \frac{V}{N}=\frac{μ}{ρN_{A}} $ И тогда находим
$ d = \sqrt{\frac{V}{N}}=\sqrt{\frac{10^{-5}}{3,34×10^{23}}}=\sqrt{\frac{μ}{ρN_{A}}}=3,11×10^{-10} м $ Ответ:
$ 3,34×10^{23} - число молекул; $
$ 2,99×10^{-26} кг - масса молекулы $ и
$ размер молекулы 3,11×10^{-10} м $ КомментарииВо сколько раз изменится подъемная сила аэростата
Данные задачи: аэростат наполняется газом
Подъемная сила
$ \vect{F} = sqrt{4x} $ - это результирующая двух сил: - вталкивающей силы
$ \vect{F_{A}} $ и силы тяжести
$ \vect{mg} $ Уравнение подъемной силы
$ \vect{F} = \vect{F_{A}}+\vect{mg} $ или
$ F = F_{A}-mg $ По закону Архимеда выталкивающая сила
$ F_{A} = ρ_{в}gV $ Где:
$ ρ_{в} - плотность воздуха $ и
$ V - объем аэростата $ В данном случае, подъемная сила аэростата будет изменяться из-за изменения массы газа внутри аэростата:
$ F_{1} = F_{A}-m_{1}g=ρ_{в}gV-m_{1}g $ где:
$ F_{1} - подъемная сила аэростата с водородом $ и
$ m_{1} - масса водорода; $ и
$ F_{2} = F_{A}-m_{2}g=ρ_{в}gV-m_{2}g $ где:
$ F_{2} - подъемная сила аэростата с гелием $ и
$ m_{2} - масса гелия $ Найдем отношение
$ \frac{F_{1}}{F_{2}} = \frac{g(ρ_{в}V-m_{1})}{g(ρ_{в}V-m_{2})}=\frac{m_{в}-m_{1}}{m_{в}-m_{2}} $ где:
$ m_{в} - масса воздуха вытесняемая аэростатом $ Величины m_{1}, m_{2} и m_{в} можно определить из уравнения Менделеева-Клапейрона, считая параметры P, V и T одинаковыми для всех газов
$ PV = (\frac{m}{μ})RT $ Тогда
$ \frac{m_{в}-m_{1}}{m_{в}-m_{2}}=\frac{μ_{в}-μ_{1}}{μ_{в}-μ_{2}} $ где
$ μ_{1}, μ_{2}, μ_{в} - молярные массы водорода, гелия, воздуха $ И окончательно
$ \frac{F_{1}}{F_{2}} = \frac{μ_{в}-μ_{1}}{μ_{в}-μ_{2}}=\frac{29-2}{29-4}=1,08 $ Ответ:
$ Подъемная сила уменьшится в 1,08 раза $ КомментарииЧему равна плотность тела?
Данные задачи: тело погруженное в воду
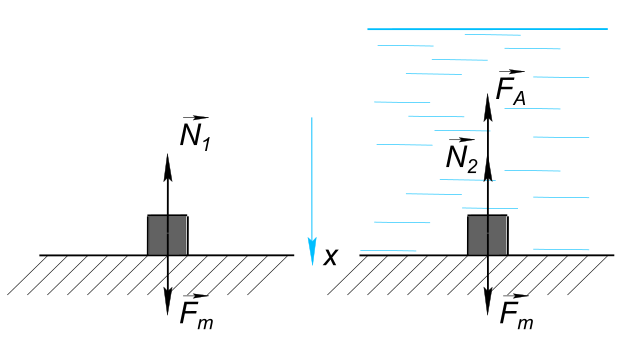
Изобразим на рисунке условия задачи В воздухе на тело действуют две силы: - сила тяжести;
$ \vect{F_{т}} = \vect{mg} $ и сила реакции опоры
$ \vect{N_{1}} = - \vect{P_{1}} $ Модуль
$ P_{1} = N_{1} $ Выталкивающей силой воздуха можно пренебречь, ввиду ее малости. Тогда условие равновесия тела будет иметь вид
$ \vect{N_{1}}+\vect{mg} = 0 $ или в проекции на ось x
$ mg-N_{1} = 0 $ или
$ mg = N_{1} = P_{1} $ Но
$ P_{1} = ρ_{т}gV $ В воде на тело действуют три силы: - сила тяжести;
$ \vect{F_{т}} $ - сила реакции опоры
$ \vect{N_{2}} = - \vect{P_{2}} $ или
$ P_{2} = N_{2} $ и выталкивающая сила
$ F_{A} = ρ_{в}gV $ Условие равновесия тела будет
$ \vect{F_{т}}+\vect{N_{2}}+\vect{F_{A}} = 0 $ или в проекции на ось x, это уравнение примет вид
$ F_{т}-N_{2}-F_{A} = 0 $ или
$ P_{2} = ρ_{т}gV_{т}-ρ_{в}gV $ по условию
$ P_{1} = nP_{2} $ подставляем
$ \frac{ρ_{т}gV}{n}=ρ_{т}gV_{т}-ρ_{в}gV $ и
$ ρ_{т}(\frac{V}{n}-V_{т})=-ρ_{в}V $ или
$ ρ_{т}(V_{т}-\frac{V}{n})=ρ_{в}V $ делим на V
$ ρ_{т}(1-\frac{1}{n})=ρ_{в} $ и окончательно
$ ρ_{т}(1-\frac{1}{n})=ρ_{в}\frac{n}{n-1}=1000\frac{3}{3-1}=1500 \frac{кг}{м^{3}} $ Ответ:
$ плотность тела равна 1500 \frac{кг}{м^{3}} $ КомментарииВо сколько раз площадь большого поршня гидравлического пресса больше площади малого?
Данные задачи: При подъеме груза с помощью гидравлического пресса, была затрачена работа
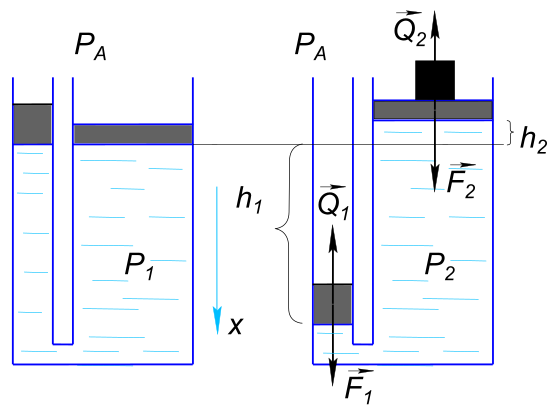
Изобразим на рисунке условия задачи Первоначально нагрузка не давит на большой поршень
$ P_{1} = давление жидкости в обеих коленах $ Затем за 10 ходов было создано давление жидкости в обеих коленах
$ P_{2} = \frac{F_{2}}{S_{2}} $ При выполнении 10 ходов перемещение малого поршня
$ h_{1} = nh $ перемещение большого поршня
$ h_{2} $ Так как
$ P_{2} = \frac{F_{1}}{S_{1}}=\frac{F_{2}}{S_{2}} $ Работа совершенная при выполнении 10 ходов по перемещению малого поршня
$ A = Q_{1}h_{1}=F_{1}nh $ Сила Q2, получаемая с помощью гидравлического пресса, должна быть больше или равна силе тяжести груза
$ Q_{2}=F_{2} = mg $ Так как
$ F_{1}=\frac{A}{nh}=\frac{S_{1}}{S_{2}}F_{2}=\frac{S_{1}}{S_{2}}mg $ Откуда
$ \frac{S_{1}}{S_{2}}=\frac{A}{mgnh} $ И окончательно
$ \frac{S_{2}}{S_{1}}=\frac{mgnh}{A}=\frac{2000×10×10×0,1}{40}=500 $ Ответ:
$ Площадь большого поршня в 500 раз больше - малого $ КомментарииКакая должна быть высота ртути, налитой в трубку, чтобы пластинка отпала?
Данные задачи: Стеклянная трубка, закрытым пластинкой нижним концом, опущена воду в вертикальном положении
До погружения в воду на пластинку действует с обеих сторон одинаковые и противоположно направленные силы, вызванные атмосферным давлением, которые уравновешивают друг друга. В погруженном положении на пластинку действуют две противоположно направленные силы:
$ F_{1} - сила давления ртути $ и
$ F_{2} = сила давления воды $ Пластинка отпадет, когда
$ F_{1} >= F_{2} $ или
$ P_{1} >= P_{2} $ Так как
$ F = PS $ Где
$ S - площадь сечения трубки $ Но
$ P_{1} = P_{А}+ρ_{1}gh_{1} $ и
$ P_{1} = P_{А}+ρ_{2}gh_{2} $ Тогда
$ P_{А}+ρ_{1}gh_{1}=P_{А}+ρ_{2}gh_{2} $ Откуда находим
$ h_{1} = \frac{ρ_{2}h_{2}}{ρ_{1}}=\frac{1×10^{3}×0,68}{13,6×10^{3}}=0,05 м $ Ответ:
$ Высота налитой ртути >=0,05 м $ КомментарииНайти изменение импульса
Данные задачи: шар свободно упал на горизонтальную площадку
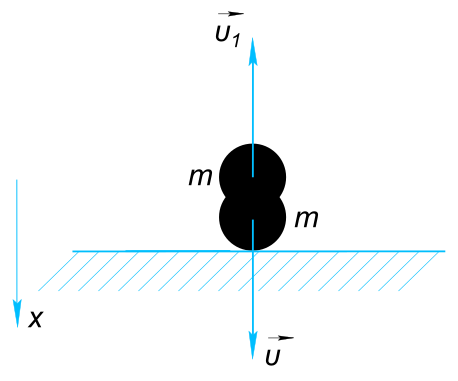
Изобразим на рисунке условия задачи Шар после абсолютно упругого удара отскочит с той же по величине скоростью, что была у него до удара, но противоположной по направлению.
$ \vect{υ_{1}} $ Ось x направим вниз. До взаимодействия с площадкой импульс шара
$ \vect{P_{1}} $ направлен по оси x (как вектор). После удара импульс шара направлен по вектору скорости υ1
$ \vect{P_{2}} $ Найдем проекции импульсов на ось x и тогда
$ ∆P = P_{1}-(-P_{2}) $ Учитывая, что
$ P_{1}=P_{2} $ Находим
$ ∆P_{1} = P-(-P)=2P=2mυ=2×0,1×10= 2 кг\frac{м}{с} $ При абсолютно не упругом взаимодействии, шар не отскочит от площадки. Изменеие импульса
$ ∆P_{2} = P-(0)=P=mυ=0,1×10=1кг\frac{м}{с} $ Ответ:
$ изменение импульса шара ∆P_{1}=2 кг\frac{м}{с} $
$ изменение импульса шара ∆P_{2}=1 кг\frac{м}{с} $ КомментарииНайти период обращения шарика
Данные задачи: Шарик, подвешенный к потолку на нити, описывает окружность в горизонтальной плоскости
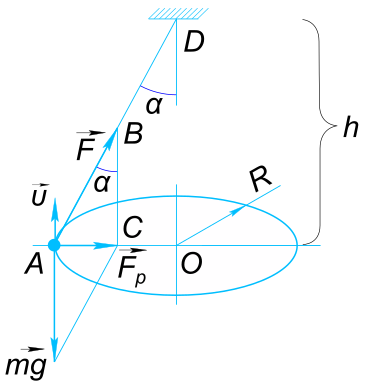
Изобразим на рисунке условия задачи Силы действующие на шарик:
$ \vect{mg} - сила тяжести; $ формула 2
$ \vect{F} - сила натяжения нити. $ Изображается диагональю параллелограмма
$ \vect{F_{р}} - равнод. сил тяжести и натяжения нити $ Запишем закон движения (второй закон Ньютона)
$ F_{р} = ma $ Где
$ a = \frac{υ^{2}}{R} $ и учитывая,что
$ υ = \frac{2πR}{T} $ получаем
$ F_{р} = m(\frac{4π^{2}}{T^{2}})R $ Из треугольника ABC
$ F_{р} = mgtg(α) $ Из треугольника ADO
$ tg(α) = \frac{R}{h} $ Тогда можем записать
$ mg\frac{R}{h} = m(\frac{4π^{2}}{T^{2}})R $ откуда находим
$ T = 2π\sqrt{\frac{h}{g}}=2×3,14×\sqrt{\frac{1,25}{9,81}}=2,24 с $ Ответ:
$ период обращения шарика равен 2,24 с $ КомментарииКакую наименьшую скорость, в верхней точке «мертвой петли» должен иметь самолет, чтобы не свалиться в «штопор»
Данные задачи: самолет выполняет «мертвую петлю»
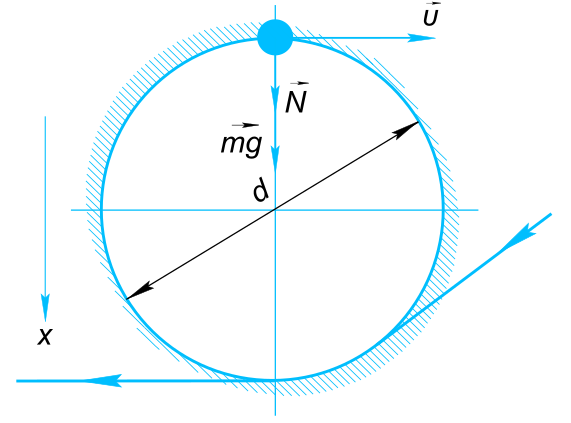
Изобразим на рисунке условия задачи В верхней точке на самолет действует сила тяжести
$ \vect{mg} $ и реакция опоры (самолет летит опираясь крыльями на воздух)
$ \vect{N} $ Направим ось x вертикально вниз и запишем уравнение движения самолета в проекции на данную ось
$ N+mg = ma $ Где
$ a - центробежное ускорение $ В момент прохождения верхней точки самолет и летчик находятся в состоянии невесомости
$ N = 0 $ И тогда
$ mg = ma $ Где
$ a = \frac{υ^{2}}{R}=\frac{υ^{2}}{\frac{d}{2}} $ Откуда находим
$ υ = \sqrt{g\frac{d}{2}}=\sqrt{9,81\frac{510}{2}}=50 \frac{м}{с} $ Ответ:
$ наименьшая скорость самолета равна 50 \frac{м}{с} $ КомментарииНайти массы тел, их ускорения и силу натяжения нити
Данные задачи: Два тела связаны невесомой и нерастяжимой нитью, перекинутой через блок, подвешенный на пружинных весах (динамометре)
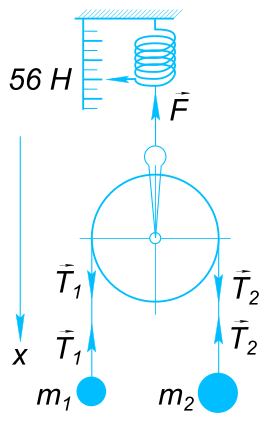
Изобразим на рисунке условия задачи На тело массой m1 действует сила тяжести
$ \vect{m_{1}g} $ и сила натяжения нити
$ \vect{T_{1}} $ На тело массой m2 действует сила тяжести
$ \vect{m_{2}g} $ и сила натяжения нити
$ \vect{T_{2}} $ На блок действует силы натяжения нитей
$ \vect{T_{1}} и \vect{T_{2}} $ и сила упругости пружины динамометра
$ \vect{F} $ Направим ось x вертикально вниз и запишем уравнение движения каждого тела в проекциях на данную ось
$ m_{1}g - T_{1} = - m_{1}a_{1} $
$ m_{2}g - T_{2} = m_{2}a_{2} $
$ T_{1} + T_{2} - F = 0 $ Если принять массу блока равной нулю, а нить невесомой и не растяжимой, то
$ |\vect{T_{1}}| = |\vect{T_{2}}|=T $ и
$ a_{1} = a_{2} = a $ Тогда уравнения примут вид
$ m_{1}g - T = - m_{1}a $
$ 2m_{1}g - T = 2m_{1}a $
$ 2T - F = 0 $ Откуда находим
$ T = \frac{F}{2} = \frac{56}{2} = 28 Н $ Приравняв
$ m_{1}(g+a) = 2m_{1}(g-a) $ Откуда, раскрыв скобки, находим
$ a = \frac{g}{3} = \frac{9,81}{3} = 3,3 \frac{м}{с^{2}} $ и
$ m_{1} = \frac{T}{g+a} = \frac{T}{g+\frac{g}{3}} = \frac{3T}{4g} = \frac{3×28}{4×9,81} = 2,14 кг $
$ m_{2} = 2m_{1} =2×2,14 =4,28 кг $ Ответ:
$ Ускорение тел 3,3 \frac{м}{с^{2}}, масса тел 2,14 кг и 4,28 кг $ КомментарииНайти угловую скорость и частоту вращения барабана лебедки
Данные задачи: груз поднимается с помощью лебедки
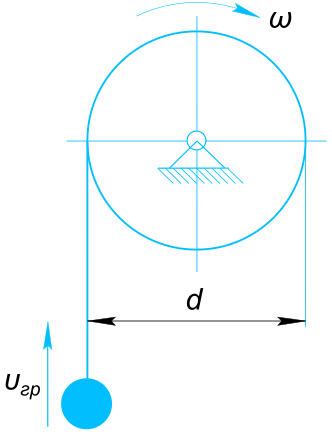
Изобразим на рисунке условия задачи Как видно из рисунка радиус вращения точки на поверхности барабана
$ r = \frac{d}{2}=\frac{0,16}{2}=0,08 м $ Угловая скорость связана с частотой вращения соотношением
$ ω = 2πn = 2π(\frac{N}{t}) $ Где:
$ t - время вращения; $
$ N - количество оборотов за время вращения $ Линейная скорость
$ υ_{гр} = \frac{2πr}{T} $ Где:
$ T - время совершения одного оборота $ Откуда находим
$ T = \frac{2πr}{υ_{гр}} $ Тогда
$ n = \frac{1}{T} = \frac{υ_{гр}}{2πr}=\frac{0,628}{2×3,14×0,08}=1,25 с^{-1} $ И
$ ω = 2πn = 2×3,14×1,25 = 7,85 \frac{рад}{с} $ Ответ:
$ Частота вращения барабана лебедки 1,25 с^{-1}; $
$ Угловая скорость 7,85 \frac{рад}{с}. $ КомментарииОпределить угловую и линейную скорости и центростремительное ускорение
Данные задачи: Точки земной поверхности, расположенные на полюсе, экваторе и широте 45°
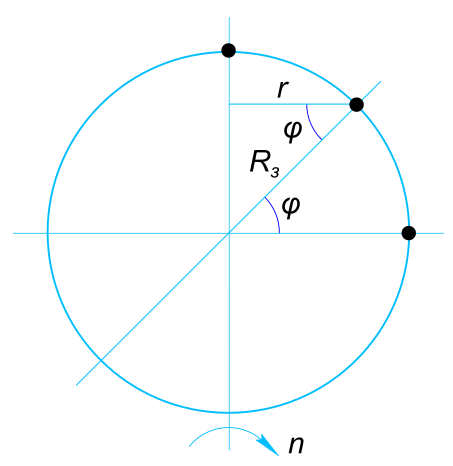
Изобразим на рисунке условия задачи Как видно из рисунка радиус вращения точки на земной поверхности
$ r = R_{З}cos(φ) $ Все точки земной поверхности совершают полный оборот за период времени T равный суткам. Поэтому угловая скорость
$ ω = \frac{2π}{T}=\frac{2×3,14}{8,64×10^4}=7,26×10^{-5} с^{-1} $ одинакова для всех точек. Линейная скорость по определению
$ υ = \frac{2πr}{T} $ или
$ υ_{φ} = \frac{2πR_{З}}{T}cos(φ) $ Центростремительное ускорение
$ a_{ц} = \frac{(υ_{φ})^{2}}{r} $ Подставляя значения угла в полученные уравнения находим:
$ на полюсе: φ = 90°, υ=0, a_{ц}=0; $
$ на широте 45°: φ = 45°, υ=326 \frac{м}{с}, a_{ц}=2,38×10^{-2}\frac{м}{с^2}; $
$ на экваторе: φ = 0°, υ=465 \frac{м}{с}, a_{ц}=3,4×10^{-2}\frac{м}{с^2} $ КомментарииЧерез какое время пароходы друг для друга скроются из вида
Данные задачи: Курсы двух пароходов плывущих в море пересеклись
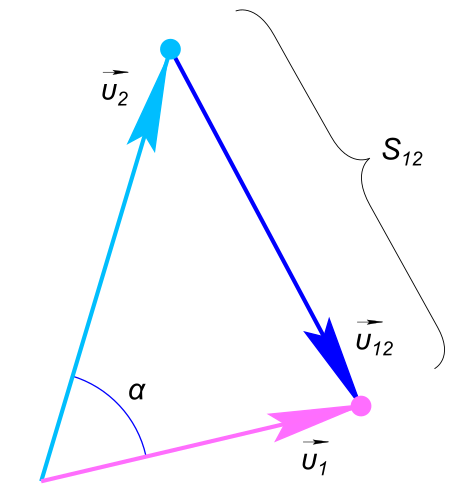
Изобразим на рисунке условия задачи Рассмотрим движение первого парохода в двух системах отсчета, одна из которых связана с землей и поэтому неподвижна, а другая связанная со вторым пароходом - движущаяся относительно берега равномерно и прямолинейно. Тогда, в соответствии с классическим законом сложения скоростей
$ \vect{υ_{1}} = \vect{υ_{2}}+\vect{υ_{12}} $ Где
$υ_{1} и υ_{2}$ - скорости пароходов в системе отсчета, связанной с берегом; скорость первого парохода в системе отсчета, связанной со вторым кораблем.
$υ_{12}$ Отсюда
$ \vect{υ_{12}} = \vect{υ_{1}}-\vect{υ_{2}} $ Из векторного треугольника по теореме косинусов находим модуль
$ |\vect{υ_{12}}| = \sqrt{(υ_{1})^{2}+(υ_{2})^{2}-2υ_{1}υ_{2}cos(α)}=20,42 \frac{км}{ч} $ Тогда
$ τ = \frac{S}{υ_{12}} = \frac{S}{\sqrt{(υ_{1})^{2}+(υ_{2})^{2}-2υ_{1}υ_{2}cos(α)}}=0.49 ч $ Ответ:
$ пароходы скроются из вида друг для друга через 0,49 ч $ КомментарииНайти ускорение движения бруска и силу натяжения нити
Данные задачи: брусок скользит по горизонтальной плоскости
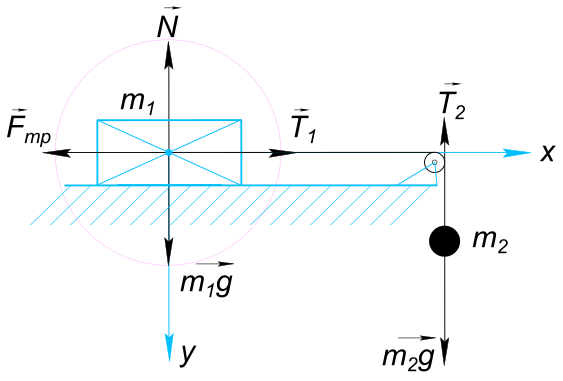
Изобразим на рисунке условия задачи На брусок действуют силы: Сила тяжести
$ m_{1}g $ Сила нормальной реакции опоры
$ N $ Сила натяжения нити
$ T_{1} $ Сила трения
$ F_{тр} $ На груз действуют силы: Сила тяжести
$ m_{2}g $ Сила натяжения нити
$ T_{1} $ Запишем для бруска и для груза уравнения в векторной форме
$ \vect{m_{1}g}+\vect{N_{}}+\vect{T_{1}}+\vect{F_{тр}} = \vect{m_{1}a_{1}} $
$ \vect{m_{2}g}+\vect{T_{2}} = \vect{m_{2}a_{2}} $ Спроецируем силы действующие на брусок на выбранные направления осей x и y, получим: ось x:
$ T_{1}-F_{тр} = m_{1}a_{1} $ ось y:
$ m_{1}g - N = 0 $ Из уравнения для оси y
$ m_{1}g = N $ Поэтому
$ F_{тр} = μN = μm_{1}g $ Тогда уравнение для оси x принимает вид
$ T_{1}-μm_{1}g = m_{1}a_{1} $ Спроецируем силы действующие на груз на направление оси y, получим: ось y:
$ m_{2}g - T_{2} = m_{2}a_{2} $ Так как нить невесомая и нерастяжимая, а масса блока пренебрежимо мала, поэтому
$ T_{1} = T_{2} = T $ и
$ |a_{1}| = |a_{2}| = a $ Тогда уравнения для бруска и для груза принимаю вид
$ T - μm_{1}g = m_{1}a $
$ m_{2}g - T = m_{2}a $ Решаем их как систему уравнений:
$ m_{2}g - m_{2}a = T $ тогда
$ m_{2}g - m_{2}a - μm_{1}g = m_{1}a $ и
$ (m_{2} - μm_{1})g = (m_{2}+m_{1})a $ откуда
$ a = \frac{(m_{2} - μm_{1})g}{m_{2}+m_{1}}=\frac{(0,5 - 0,1×2)×10}{0,5+2}=1,2 \frac{м}{с^{2}} $ и
$ T = m_{2}(g - a) = 0,5×(10 - 1,2) = 4,4 Н $ Ответ:
$ Ускорение движения бруска 1,2 \frac{м}{с^{2}} $ и
$ Сила натяжения нити 4,4 Н $ КомментарииОпределить величину и направление ускорения лифта
Данные задачи: опускающийся лифт с грузом
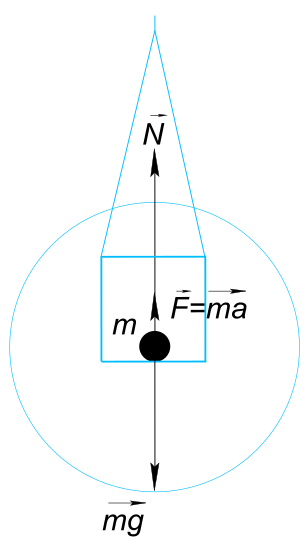
Изобразим на рисунке условия задачи формула 1
$ Σ\vect{F} = \vect{mg}+\vect{N} $ или
$ ma = mg-N $ Откуда находим
$ a = g-\frac{N}{m}=9,81-\frac{1440}{140}=-0,48 \frac{м}{с^{2}}$ Ответ:
$ Ускорение лифта 0,48 \frac{м}{с^{2}} и оно направлено вверх $ КомментарииС какой силой нужно действовать на тело, чтобы оно падало вертикально вниз с ускорением 15 м/c2
Данные задачи: тело падает вертикально вниз
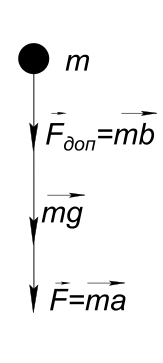
Изобразим на рисунке условия задачи На тело действуют две силы
$ Σ\vect{F} = \vect{mg}+\vect{mb} $ где
$ b - ускорение от силы F_{доп} $ Тогда
$ ma = mg+mb $ Откуда
$ b = a-g $ Тогда
$ F_{доп} = m(a-g)= 5(15-10)=25 Н $ Ответ:
$ на тело нужно действовать вниз силой 25 Н $ КомментарииОпределить положения центра тяжести системы шаров
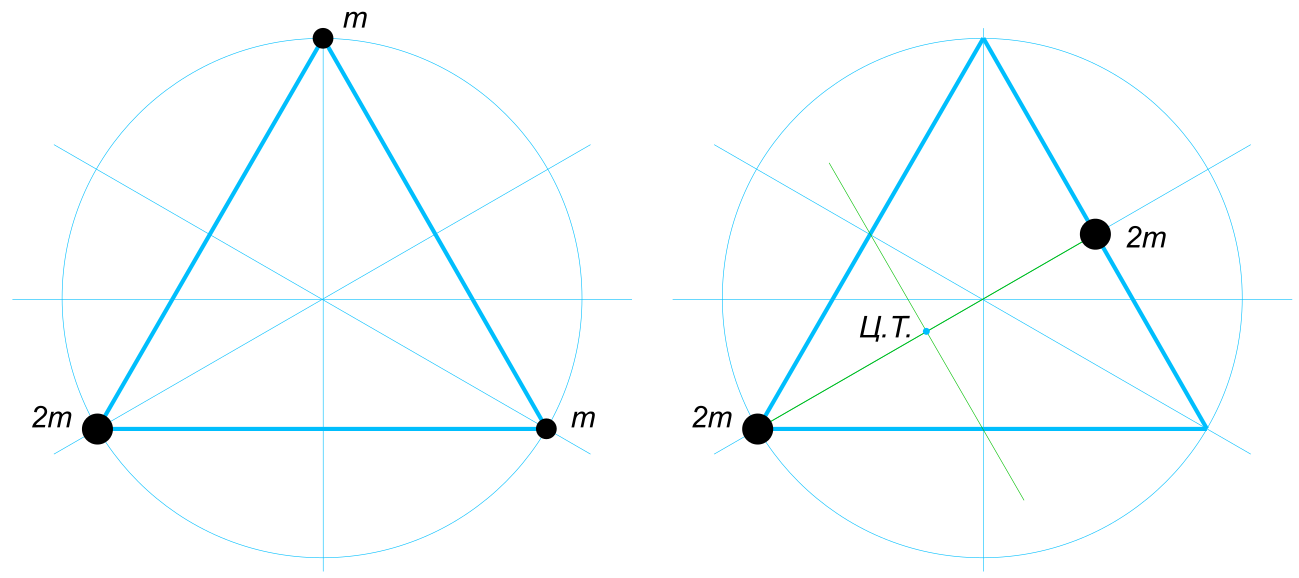
Изобразим условие задачи на рисунке Находим центр тяжести двух шаров массой m каждый
$ На середине стороны треугольника, их соединяющей $ Находим центр тяжести двух шаров массой 2m каждый. На середине
$ биссектрисы угла треугольника, их соединяющей $ Ответ: Центр тяжести этой системы шаров расположен на середине биссектрисы угла треугольника в вершине,которого находится шар массой 2m Комментарии
|
Записать новую задачу Все задачи Все темы Все физики |


Комментарии